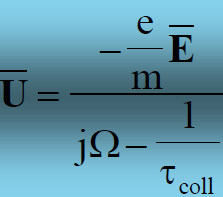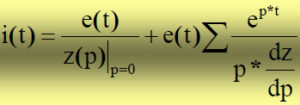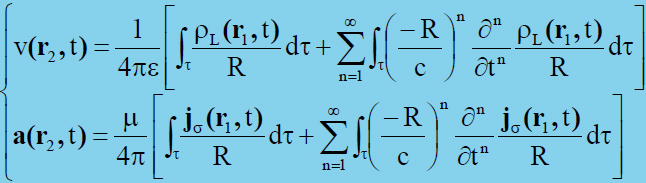I contributi italiani alla teoria dei circuiti
La teoria dei circuiti nasce con l’invenzione della Pila Voltiana è la progressiva affermazione del galvanismo
Con precise implicazioni in ambito filosofico:
L’esistenza di una molteplicità di fluidi interagenti all’interno della pila contrasta con l’idea di un universo illuministico nel quale i fluidi si adattano a vivere separati.
In contrapposizione al modello newtoniano, gli attori del fenomeno agiscono non in relazione alla loro posizione, ma, in ragione di quella che sarà chiamata corrente, in termini di movimento.
E ovviamente in ambito applicativo
La presenza di un campo elettromotore, quindi di una sorgente rotazionale, consente il movimento dei portatori liberi e dunque la conduzione.
Il regime è stazionario e dunque le bottiglia di Leida sono assenti.
Per adesso l’approccio è legato più che altro ad un generoso quanto fortunato empirismo.
Tutto è descrittivo e non esplicativo: la teoria dei circuiti, se tale può già considerarsi, procede in modo autonomo rispetto agli studi che, in termini campistici, condurranno alla Dynamical Theory.
Il dialogo con i Grandi Fisici è dunque circoscritto.
Un voltmetro (Volta nel 1801 ha dato una prima definizione di tensione) ed un amperometro (Ampere, nei primi anni ’20, è giunto a quella di corrente), complice un po’ di algebra, è quanto basta.
Per il resto, dato che il regime è stazionario e il vuoto non ha conduttività, un insieme di apparecchi connessi tra loro costituisce a priori un circuito.
Nel 1826 Ohm enuncia l’omonima legge
Nel 1841 J.P. Joule perviene all’omonima legge: il prodotto tensione per corrente esprime una potenza elettrica.
Per la verità, nel suo Über die Erhaltung der Kraft vi ritornerà nel 1847 lo stesso von Helmholtz.
Nel 1847 è poi la volta di Kirchhoff con le sue omonime leggi.
In seguito potranno essere considerate corollari propri di una lettura integrale delle equazioni di Maxwell particolarizzate al regime stazionario.
Per ora sono solo l’esito conclusivo, descrittivo e non esplicativo, di un’evidenza sperimentale;
Topologia (Kirchhoff) e tipologia (Ohm), combinandosi, danno la soluzione della rete elettrica.
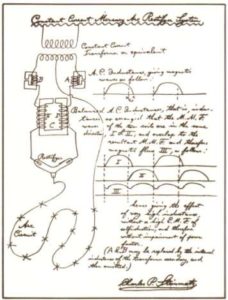
Sono interessanti al riguardo i seguenti appunti di Heaviside e di Steinmetz:
Sempre von Helmholtz, nel 1853, attraverso il suo principio di sovrapposizione delle cause degli effetti, formalizzerà il teorema del generatore equivalente.
Nel 1883 Thevenin ne dà la formulazione serie
Nel 1926 Norton ne dà la formulazione parallelo
In seguito, facendo il suo ingresso, la seconda rivoluzione industriale, con la sua richiesta di tecnologie elettriche, porta con sé le problematiche legate alla inderogabile necessità di passare ad un regime variabile e dunque:
- al possibile uso della fisica matematica;
- alla propria conoscenza dell’ elettromagnetismo;
Almeno all’inizio, il problema non sembra però porsi:
Nel 1853 Kelvin, studiando i cavi, elabora lagrangianamente la prima equazione relativa ad un “circuito a due energie”:
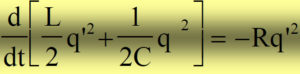
nella quale, provvisoriamente, la futura induttanza compare come una non meglio identificata capacità dinamica.
Complice il valore contenuto delle frequenze in gioco, il passaggio al regime variabile sembra automatico: scontato e senza complicazioni che non siano quelle implicite nel passaggio dalle relazioni algebriche a quelle differenziali.
Basta adottare un approccio lagrangiano e tutto, senza problemi, torna.
Dopo tutto, in un approccio che, volutamente, si mantiene descrittivo e non esplicativo (e in realtà, con l’assenza della Dynamical Theory, non può che essere così), nessuno ancora si rende che l’approccio circuitale a costanti concentrate è espressione di un’azione a distanza in uno spazio geometrico.
Le equazioni di un regime variabile giudicato corretto a priori sembrano moltiplicarsi;
Assumono particolare importanza in queglia nni gli studi di Kelvin, Helmholtz e Siemens;
È di interesse però la riserva con cui Fleming, uno degli assistenti del Maestro, commenta le relazioni circuitali di Maxwell in regime variabile:
«Maxwell, by a process of extraordinary ingenuity, extended this reasoning (the method of Lagrange) from materio-motive forces, masses, velocities and kinetic energies of gross matter, to the electromotive forces, quantities, currents and elektrokinetic energies of electrical matter, and, in so doing, obtained a similar equation of great generality for attacking electrical problems».
Ancora Maxwell, nel 1864, in margine alla sua Dynamical Theory, elabora le equazioni del mutuo induttore.
Nel 1855 Kelvin, con riferimento al cavo non induttivo, passa al modello a costanti distribuite di tipo diffusivo;
Nel 1857 sarà la volta di Kirchhoff che, in modo intuitivo dedurrà il quasi-TEM classico. Sarà però Mie, nel 1900, a dedurre per primo la teoria maxwelliana completa della linea bifilare.
In seguito, con il progredire delle esigenze della tecnologia: si avverte però sempre di più l’esigenza di una ricerca sistematica delle connecting links between pure science and practical work e dunque del legame con la Dynamical Theory
Con il tempo, l’ingegnere elettro- magnetico scientifico diventerà, a pieno titolo e a tutti gli effetti, un postmaxwelliano;
E lo farà secondo una successione del tipo seguente:
Per ora, però, l’inizio non è affatto facile:
Le difficoltà maggiori si incontrano nella messa a punto degli algoritmi circuitali e nel dualismo circuitale- campistico della teoria degli apparecchi magnetoelettrici ancora nel 1881, il postmaxwelliano Ferraris, ossservando il circuito magnetico delle dinamo Hopkinson-Edison, parlerà esplicitamente di «insegnamento della disfatta»
Non è certo questa la sede per parlarne ed in ogni caso non c’è comunque il tempo necessario per farlo;
basteranno dunque alcune citazioni, tratte dalla letteratura dell’epoca, per capire, anche a livello di accettazione del nuovo ruolo di ingegnere elettromagnetico, le difficoltà non trascurabili di quell’esordio:
Innanzitutto, da parte degli altri rami dell’ingegneria, con grande senso della solidarietà, non si mancava di osservare che: «electrical engineering was born yesterday and had no long- standing tradition, no professional culture»
Il che, a conti fatti, al di là di ogni priorità scientifica, altro non esprimeva, “classicamente”, che una ben precisa esigenza di controllo del territorio.
Dopo tutto, nei secondi anni ’80, l’accordo tra la German Edison Company e la Siemens & Halske si era tradotto nella pubblicazione, da parte di Erasmus Kittler:
Di un Handbuch der Elektrotechnik il quale, con una sorprendente lungimiranza, era già suddiviso in due tomi:
- Starstromtechnik
- Schwachstromtechnik
In realtà, almeno in quei primi anni ’80 qualche fondamento a quelle riserve però c’era.
Anche a prescindere dal fatto che, per combattere le correnti parassite, qualche ingegnere “illuminato” aveva proposto di sostituire i nuclei ferromagnetici con nuclei di legno. E che un ufficio brevetti USA aveva respinto una richiesta di brevetto di un trasformatore perché l’elevazione della tensione al secondario era giudicata incompatibile (SIC!) con il principio di conservazione dell’energia. Restava comunque il fatto che, nel 1888, calcolando il rapporto v(t)/i(t), un ingegnere telegrafista americano aveva affermato che: «it is a well known fact that alternating currents do not follow Ohm’s law, and nobody knowns what law they follow»
Nel 1864 Maxwell aveva dimostrato esattamente il contrario.
========31========
Ma, a parte ogni altra considerazione, chi avesse letto il
semplicissimo modello di Drude della conduzione
classicamente basato sulla quantità di moto :
avrebbe trovato, avvalendosi del metodo degli esponenziali complessi, un legame tra campo elettrico e velocità delle cariche così esprimibile:
E dunque tale, essendo t=10-14 da poter essere assimilato al legame proprio del regime stazionario
Il realtà il problema era assai più complesso L’impiego della corrente alternata, imposto dall’uso del trasformatore, metteva in gioco il calcolo differenziale;
Un approccio che gli ingegneri USA dell’epoca non conoscevano, occorreva dunque rendere algebriche le equazioni differenziali oppure mandare di nuovo a scuola gli ingegneri.
A questo le riflessioni di Steinmetz, a mathematical physic who began to be an engineer, sono immediate:
«the electrical engineering is the most mathematical of all engineering disciplines»
«at present all mathematical and analytical theories [of AC circuits] especially if they have to start from solution of differential equations, are still of very little value for the practical engineer, who is not yet generally expected to master the powerful weapons of mathematics»
Riconosciuto che:
«the electrical engineering is the most mathematical of all engineering disciplines»
le riflessioni di Steinmetz, a mathematical physic who began to be an engineer, sono immediate e, movendo dal metodo degli esponenziali complessi di von Helmholtz, conducono all’algebra dei fasori:
« I do not refer to practical men in very limited sense of anti-or extra-theoretical, but to theoretical men who desire to make theory practically workable».
«engineers could treat complex-number impedance in AC circuits like resistance in DC circuits».
Con il preciso scopo di:
«to try to generate electricity from square root of minus one»
Le complex quantities di Steinmetz e di Berg avrebbero totalmente risolto il problema:
In modo analogo, con Heaviside, sarebbe stato introdotto il calcolo operatoriale.
La ricerca di Heaviside sarà portata avanti da Ernst Julius Berg, il braccio destro di Steinmtez. Nel 1926 il suo trattato sulle L- trasformate ha, sul piano applicativo già l’assetto attuale.
L’analisi dinamica dei circuiti proseguirà poi con Steinmetz Il suo opus magnum sarà pubblicato nel 1909 ed avrà come titolo:
“Theory and calculation of transient phenomena and oscillation”
Analoghe considerazioni, con anche maggior vicinanza a Maxwell, valgono poi per le apparecchiature magnetoelettriche.
E, al momento di mettere a punto le design equations, passando dagli ironless coils della dynamical philosophy scozzese ai circuiti ferromagnetici veri
Il lascito maxwelliano non basta più, perché, finalizzato all’analisi e non alla sintesi, esso effettua la partizione degli impulsi di tensione ai morsetti secondo il metodo delle induttanze, cioè in autoflussi e flussi mutui, mentre, mettendo a punto il metodo di campo, la partizione deve essere
fatta in flusso comune e flussi dispersi:
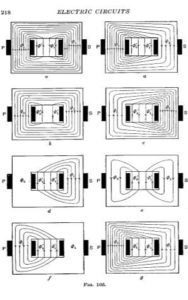
Dai disegni di Steinmetz: il senso postmaxwelliano del fisico matematico che diviene ingegnere elettromagnetico.
Ne nascono sensi di disagio; Le citazioni di cui nel seguito ben rendono la misura di questo stato d’animo.
«the maxwellian theory of the transformer described a device that does not exist in practise, but merely haunts as a phantom transformers the text-books and mathematical treatise on transformers».
“most theories of the induction motor were written only by theorist who never constructed a motor themselves and who have never seen a motor taken apart” .
“phantom transmission lines circuit of uniformly distributed capacity and inductance was very different from the circuit exitenting in practis”.
E pur tuttavia si ribadisce che:
«Attemps of ordinary mortals to do better than Maxwell did must discouraged. Let us follow Maxwell as long as we can, then, when someone is born who is more profound than Maxwell, we will bow him».
La ricerca, colta nel suo dualismo campistico-circuitale, sarebbe andata avanti. Con due contributi essenziali:
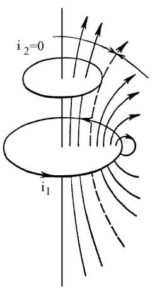
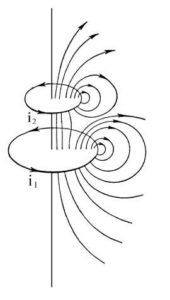
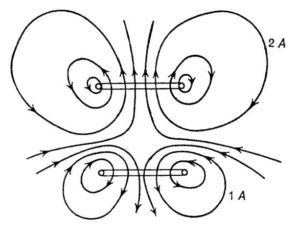
Nel 1930, usando una bobina di Helmholtz, il paradosso di Weber
L’approccio circuitale sarebbe definitivamente risultato agnostico:
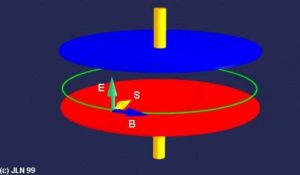
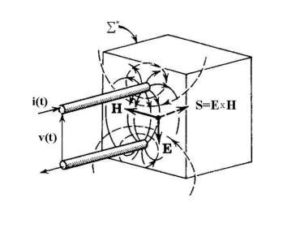
Il teorema di Poynting
Sarebbe stato riformulato da Slepian in una forma più adatta alla teoria dei circuiti
Nel 1941 Kron elabora una rete elettrica equivalente associata alle equazioni di Maxwell.
La teoria delle reti viene finalmente inquadrata nella teoria dei campi e, in termini di potenziali ritardati, considerata come una teoria approssimata:
La soluzione generale è così espressa:
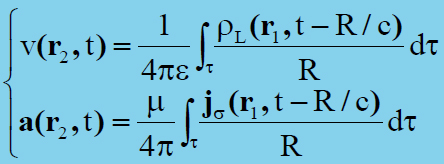
Sviluppando in serie di potenze si vede che il potenziale attuale costituisce solo il primo addendo
Nel 1927 J.R. Carson avrebbe dato il primo inquadramento della teoria dei circuiti all’interno della Dynamical Theory
Il circuito sarebbe stato preventivamente immerso in uno spazio fisico.
Sarebbero state Formalizzate le condizioni di Max Abraham
E il tema sarebbe Diventato un Corso presso il MIT
Lan Jen Chu avrebbe portato aventi il discorso parallelo
L’approccio, non certo privo dei controesempi di Shelkunoff, sarebbe inevitabilmente rimasto quantitativo e non qualitativo.
Come tale non del tutto soddisfacente Fino al punto da far definire, secondo Domina Spencer, l’approccio circuitale “a procusterian bed”
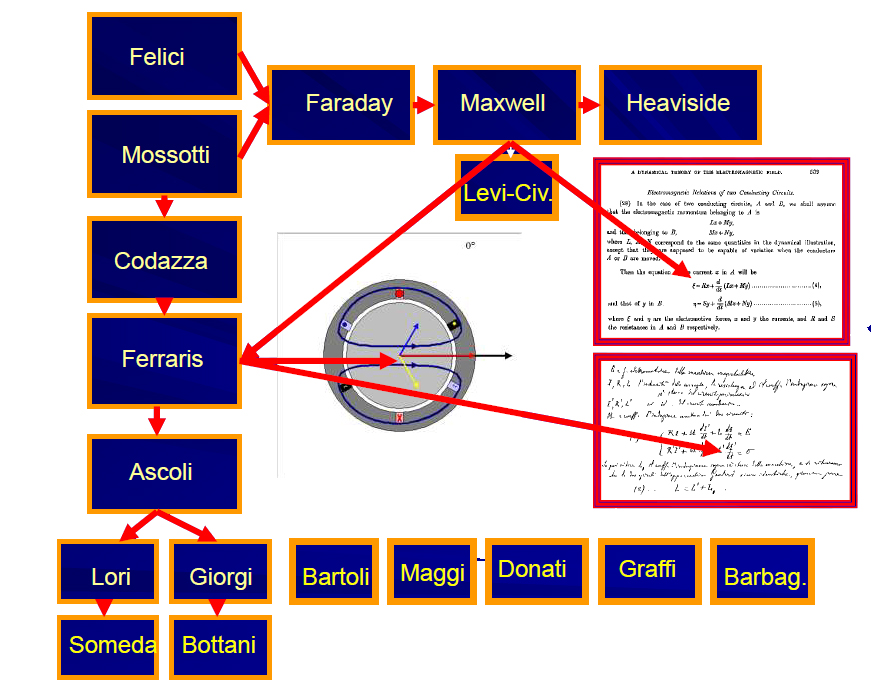
I contributi italiani vanno a collocarsi esattamente nel percorso fin qui indicato.
Per meglio comprenderne il senso conviene contestualizzare preliminarmente il contributo italiano nella Dynamical Theory scozzese.
Ferraris
- Elabora la teoria maxwelliana del trasformatore;
- Imposta una prima teoria circuitale delle perdite per isteresi
- Elabora la formula della potenza attiva
- Fa le prime riflessioni sul concetto di potenza virtuale
- Con la sua rielaborazione di Fresnel anticipa la trasformata di Fortescue;
- ========64========
Donati
- Prosegue negli studi sulla potenza virtuale
Barbagelata
- Elabora il metodo delle quattro letture nella misura della potenza polifase;
- Dà contributi di chiarimento alla nozione di potenza deformante elaborata da Budeanu;
Graffi
- Elabora, in modo indipendente da Carson la transizione campi-reti e vi aggiunge le correnti parassite;
Giorgi
Perfeziona l’algebra dei fasori;
Sviluppa la teoria della propagazione via cavo;
Formalizza e rende rigorosa la teoria del calcolo operatoriale lasciata incompiuta da Heaviside;
Dà contributi essenziali ai fondamenti della teoria elettromagnetica
========68========
Torniamo al riguardo all’ esperimento di Hertz sulla verifica sperimentale dell’esistenza delle onde elettromagnetiche
Le critiche di Poincarè, legate all’uso improprio che Hertz fece dell’integrale di Neumann nel calcolo della frequenza naturale, furono terribili e costituirono una seria minaccia per l’intera struttura elettromagnetica…
Ne seguì la lettera di Heaviside ad Hertz nella quale già si configura il concetto di regime quasi-stazionario
La loro concettualizzazione portò alle due impostazioni seguenti:
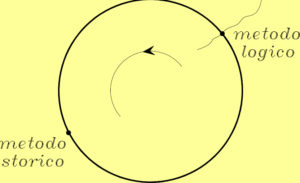
Il metodo storico
- Il fisico francesce Cornu propone di partire dalla bilancia di torsione, di arrivare alla Dynamical Theory e da questa, come sottocaso, ai circuiti
Il metodo logico
- Il misurista inglese J. Perry propone invece di partire dalle grandezze integrali (tensiometro e reometro) e da queste risalire alle leggi di campo
Sotto l’aspetto fondazionale la situazione era assai complessa e l’episodio di cui nel seguito, relativo nientemeno che a Ferraris, ce ne dà una conferma
La scienza europea, in piena crisi, decide di affidarsi a colui che in quel momento sembra saperla lunga più di ogni altro:
Giovanni Giorgi, ingegnere di 23 anni
Dopo matura riflessione, Giorgi, nell’aprile del 1894 pubblica su Electrician un articolo dal titolo “The foundations of electrical science” che può costituire il fondamento della moderna ingegneria elettromagnetica.
Secondo lui una scienza compiuta è assimilabile ad una circonferenza che può essere tagliata in modo arbitrario in un punto qualunque:
I due metodi indicati da cornu e da Perry pertanto si equivalgono.
Giorgi elabora allora quello proposto da Perry: partendo da grandezze integrali, egli, con l’uso di un tensiomentro e di un reometro stabilisce l’intera teoria circuitale e da lì, passando attraverso domini di integrazione sempre più piccoli, passa all’approccio campistico.
Nel 1926 pubblica, prima espressione di tale approccio all’elettromagnetismo, il suo trattato di fisica-matematica dei circuiti:
In esso il primo tomo riguarda la teoria dei circuiti ed il secondo, dedotta dai contenuti del primo, la teoria dei campi.
Nel primo la presentazione si basa sull’identità concetto-operazione elaborata da Bridgman.

Il metodo giorgiano si afferma e si diffonde fino a rappresentare una vera scuola di pensiero. Tra gli autori che ne resteranno influenzati: