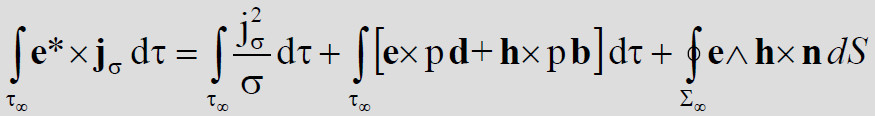Ottica
l’Ottica Il problema del concetto di spazio interessa il campo di indagine sia dell’Elettromagnetismo che dell’Ottica
Un recipiente nel quale sia estratta l’aria, anche fino al vuoto più spinto, è assolutamente trasparente tanto alla luce quanto alla propagazione dei campi elettromagnetici. La luce del sole, ad esempio, giunge fino alla terra dopo aver attraversato lo spazio vuoto.
Vediamo le caratteristiche della luce:
La luce si propaga in linea retta, inoltre subisce
- La rifrazione
- La riflessione
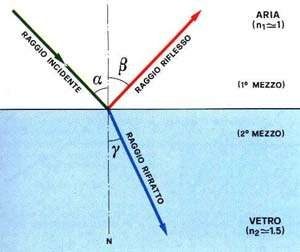
Tutti questi fenomeni, palesanti la propagazione rettilinea della luce, vengono in aiuto di una teoria corpuscolare perché tale specie di moto è proprio quella che compete ai corpuscoli Inoltre, per loro tramite, risulta possibile spiegare meccanicamente i fenomeni di riflessione e rifrazione.
Questi semplici fenomeni bastano per escogitare un’idea meccanica corpuscolare di luce.
E’ così che i concetti meccanici di sostanza, particella e fluido possono entrare nell’ottica Accanto al calorico, l’elettrico ed il magnetico, si può concepire un nuovo fluido particellare “luminoso”
Secondo tale lettura tutti i corpi luminosi emettono “particelle di luce” che, attraversando lo spazio in linea retta con velocità nota, colpiscono gli occhi e danno la sensazione luminosa esiste poi l’enigma del colore la cui soluzione corpuscolare si deve a Newton.
La luce solare è bianca ma, dopo il passaggio attraverso un prisma, essa esibisce tutti i colori esistenti nel mondo visibile Newton spiega questo fenomeno ammettendo che tutti i colori siano già presenti nella luce bianca [la quale sarebbe pertanto una miscela di specie diversa di corpuscoli] essi attraversano lo spazio astronomico e giungono a noi sotto forma di luce bianca non appena attraversano il prisma, si separano dando luogo, come nell’arcobaleno, alla dispersione della luce nei suoi vari colori.
La dispersione avvalora dunque l’ipotesi meccanico-corpuscolare
Esiste poi il problema della rifrazione, secondo la Meccanica la rifrazione è dovuta a forze risiedenti nella sostanza vetrosa del prisma. Queste debbono ritenersi differenti a seconda del tipo di corpuscoli, le più intense agendo sul violetto e le più deboli sul rosso, in tal modo ogni colore viene rifratto in modo differente ed esce dal prima separato dagli altri.
La teoria in tal modo si complica: si hanno corpuscoli di luce diversi per ogni colore… Se però la teoria è corretta, i colori separati dal prisma debbono potersi riunire se immessi in modo conveniente in un altro prisma il processo dovrà essere esattamente il reciproco del precedente e dovrà ricomporre i colori.
Newton dimostrò sperimentalmente che è possibile ottenere luce bianca dallo spettro e, tramite una successione di prismi, l’alternanza luce bianca-colori scomposti può essere ottenuta un numero
indefinito di volte.
Questi esperimenti diedero valido appoggio alla teoria secondo cui i corpuscoli appartenenti ad ogni singolo colore si comportano come sostanze inalterabili, però con tale teoria…. occorre ammettere l’esistenza di tante particelle diverse quanti solo i colori… Queste particelle, pur diverse, debbono avere nel vuoto la stessa velocità.
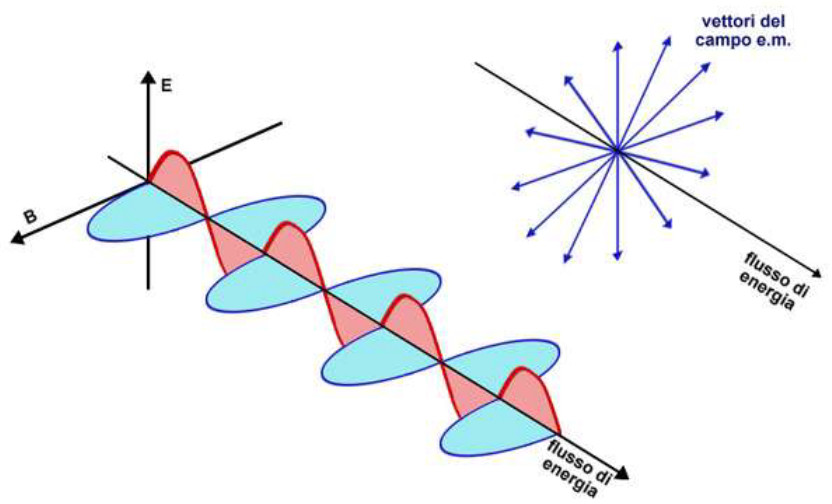
E’ possibile allora che un altro ordine di idee possa funzionare altrettanto bene senza però generare queste riserve. E’ questo il caso della teoria ondulatoria della luce secondo Huyghens la luce è un’onda Non è dunque un movimento di particelle E’ un trasferimento di energia nello spazio Non è dunque materia, ma stato dinamico Trattandosi di onde, la lettura continua ad essere meccanica.
Il presupposto essenziale della teoria ondulatoria è che lunghezze d’onda differenti corrispondono a colori differenti, in luogo dell’artificiosa separazione tra corpuscoli differenti appartenenti a colori diversi si ha la naturale differenziazioni tra lunghezze d’onda.
I corpuscoli appartenenti Le onde, di lunghezza a colori diversi hanno tutti la stessa velocità nel vuoto, ma diversa velocità nel vetro La luce bianca è una miscela di corpuscoli appartenenti a tutti i colori.
Diversa a seconda dei colori, hanno la stessa velocità nel vuoto e diversa nel vetro La luce bianca è una composizione di tutte le differenti lunghezze d’onda.
Ne segue che l’esperimento di Newton può essere descritto ed interpretato con i due diversi linguaggi.
A questo punto la decisione tra una teoria e l’altra potrebbe apparire quasi una questione di gusto e di indole, il verdetto a netto favore della teoria ondulatoria scaturì, nel XIX secolo, dalle seguenti osservazioni:
- La partizione in lunghezze d’onda era meno macchinosa di quella in corpuscoli
- La spiegazione per onde della rifrazione è più convincente Un ostacolo, se abbastanza piccolo, non deve produrre ombra. Questo è vero per la teoria ondulatoria, ma è negato dalla teoria corpuscolare
La teoria di Huyghens dunque si affermò, a questo punto sorgeva però un problema:
Se la luce consiste in oscillazioni meccaniche, il vuoto non può esistere Al suo posto deve esistere una sostanza materiale che possa fungere da supporto per le oscillazioni e la propagazione di queste stesse entro la materia, al quei tempi la teoria della propagazione in un mezzo elastico non era però particolarmente evoluta, si può anzi dire che essa cominciò ad evolvere, come parte della Meccanica, nel momento stesso in cui si affermò la teoria ondulatoria della luce.
Fino a qui, parlando di onde, i fisici si erano sempre limitati al caso delle onde longitudinali avevano in tal modo lasciato da parte quelle trasversali, in seguito Fresnel ed Arago conclusero che le vibrazioni luminose dovevano necessariamente essere trasversali. Una volta riconosciuta, e provata sperimentalmente, tale proprietà delle onde luminose, Fresnel impostò lo sviluppo di una teoria dinamica della luce che, conformemente ai metodi della meccanica, permettesse di dedurre le caratteristiche dei fenomeni ottici dalle proprietà del mezzo nel quale il fenomeno si svolgeva e delle forze in esso agenti.
Nasceva così, come evoluzione dei vortici di Cartesio, l’etere:
- quali proprietà si debbono assegnare all’etere luminifero?
- L’etere doveva essere necessariamente un solido dotato di proprietà elastiche, poiché solo in una simile circostanza potevano propagarsi onde elastiche trasversali.
Occorrono però dei requisiti particolari:
In primo luogo, a causa del grandissimo valore della velocità di propagazione c, è necessario supporre che la rigidità elastica p sia molto elevata o che la densità sia molto piccola oppure che queste due condizioni si verifichino contemporaneamente.
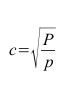
Inoltre, poiché la luce non si propaga con la stessa velocità in tutte le sostanze, si deve anche ritenere che l’etere si condensi in modo diverso all’interno dei corpi o che possa variare la sua elasticità; anche in questo caso le due circostanze possono verificarsi simultaneamente.
La prima obiezione all’ipotesi di etere elastico nasce dalla necessità di ammettere che la sua rigidità sia sufficientemente elevata da spiegare l’alta velocità delle onde. Tale sostanza offrirebbe in tal modo una notevole resistenza al moto dei corpi celesti, particolarmente dei pianeti, mentre di fatto gli astronomi non hanno mai misurato alcuna deviazione dalla legge di Newton che ne giustificasse l’esistenza.
Stokes (1845) cercò di superare questa obiezione facendo osservare che il concetto di solidità di un corpo ha in sé qualcosa di relativo: se noi colpiamo con un martello un pezzo di resina (ceralacca o di cristallo) questo si spacca in modo netto; ma se poniamo su di esso una certa massa , essa affonda in modo graduale, anche se lentissimo, nel corpo, che si comporta così come un liquido viscoso. D’altra parte le forze che intervengono nella propagazione delle onde luminose variano in tempi estremamente brevi (6*10^12 volte al secondo) rispetto alle variazioni, relativamente lente, che si verificano nei moti dei pianeti. Il rapporto tra le variazioni di questi due tipi di forza è molto più elevato di quello che si ha fra la forza impulsiva dovuta al colpo di martello e la forza di pressione dovuta al peso. Se ne conclude che l’etere può comportarsi come un solido elastico nei confronti della luce e non opporre alcuna
resistenza al moto dei pianeti.
L’etere giroscopico
Mac Cullagh (1839) portò ad un tale grado di complicazione la teoria dell’etere da rinunciare completamente al modello elastico.
Il meccanicismo …
Altamente formalizzato tramite l’opera di Fresnel, Cauchy, Arago, Stokes e Mac Cullagh, l’etere, perfezionamento dei vortici cartesiani, finì con l’assumere, per poter “esistere”, requisiti assolutamente impensabili e del tutto lontani dal quotidiano, riaffiorerà con Maxwell, il quale, con la sua suggestione neocartesiana, ne darà un modello meccanico, sarà però il canto del cigno perché nel 1882, dichiarato non osservabile, uscirà definitivamente di scena.
Verso un “lessico famigliare” comune. Dovendo in seguito parlare di “campi”, converrà richiamarne una volta per tutte, in via preliminare, le valenze fisico matematiche.
Lo faremo in una forma non del tutto elegante e rigorosa, ma certo molto più intuitiva e diretta Forse perché vicina all’approccio intuitivo degli uomini che la concepirono…
Torniamo per un attimo alla legge di Coulomb: essa rappresenta un’azione a distanza (il tempo infatti non conta…)

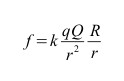
Come già quella di Newton, è descrittiva, ma non esplicativa: non dice niente del “meccanismo sottostante”… Gli attori del fenomeno (il potenziante q ed il potenziato Q) sono remoti; La variabile tempo è assente, il che vuol dire che essa è la stessa per i due attori e conseguentemente che essi si scambiano informazioni a velocità infinita; Lo spazio in cui avviene il fenomeno è estraneo all’evento: nel suo ruolo di semplice contenitore di corpi, lo spazio è puramente geometrico.
Qualora non si conoscesse la posizione del potenziante q l’approccio coulombiano sarebbe del tutto non utilizzabile Un’indicazione della strada maestra, leggendolo bene e con attenzione, è però già implicita in questo semplice passaggio algebrico:
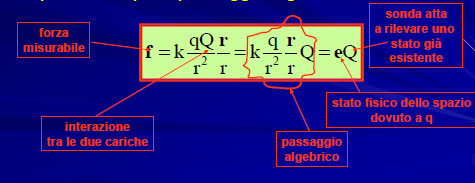
La soluzione al problema, basata proprio su tale lettura, è la teoria di campo… La teoria di campo esprime solo un cambiamento di prospettiva: il protagonista non è più la coppia di attori remoti, ma lo spazio in cui essi sono immersi
- Vediamo meglio:
- Sia in proposito il campo termico in una stanza.
- La variazione spazio-temporale della temperatura in essa misurabile è imputabile alle sorgenti di calore presenti all’interno ed all’esterno del locale.
- Se la loro natura e la loro collocazione è nota, allora, avvalendosi delle leggi della termodinamica, è possibile risalire alla funzione T(x,y,z,t) descrittiva del fenomeno.
La procedura seguita, correlando cause ed effetti tra loro remoti, rientra nella teoria dell’azione a distanza. Si spengano ora le sorgenti interne alla stanza e si assumano di natura e di collocazione incognita quelle esterne. In tal caso l’approccio precedente, non più utilizzabile, deve essere sostituito da metodi basati sulle caratteristiche di continuità e di contiguità che, come mostra senza eccezione l’esperienza, sono proprie dei campi fisici.
Per esse, nel caso termico qui considerato, la funzione incognita T(x,y,z,t) assume in ogni punto valori condizionati da quelli assunti nei punti limitrofi: se nell’intervallo to — t1 la temperatura T(P,t) varia con una certa legge, allora essa, in un punto limitrofo (P+dP), assumerà lo stesso valore in un opportuno intervallo t1 — t2.
Esiste dunque, imposta dalle proprietà costitutive di un mezzo intermedio esplicitamente compromesso con l’evento, una condizione spazio-temporale di vincolo cui, distribuendosi nello spazio ed evolvendo nel tempo, deve sottostare la grandezza T incognita.
Questa condizione è indipendente dalla natura e dalla collocazione delle sorgenti poste in punti distinti da P ed è legata in modo esclusivo alla “natura della quantità osservabile T(P,t)”. Non resta allora che mettere in equazione tale proprietà ed integrare, sulla base di assegnate condizioni iniziali ed al contorno, l’equazione differenziale spazio- temporale che ne consegue.
(Le condizioni iniziali riassumono la “storia passata” del sistema; le condizioni al contorno sintetizzano sulla frontiera del dominio di integrazione il “contributo del sistema esterno” alla frontiera stessa).
L’equazione di Fourier è ben nota:
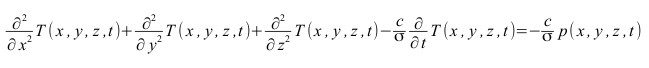
Ma a noi interessa farne solo l’anatomia:
L’incognita T(P,t) deve soddisfare l’equazione precedente senza alcun riferimento alle sorgenti di calore esterne al dominio considerato.
La scelta della temperatura T(P,t), compiuta tra le infinite soluzioni possibili, va attuata tenendo conto della distribuzione delle sorgenti nei punti esterni al dominio. Il loro contributo si traduce infatti nella assegnazione delle condizioni al contorno subordinatamente alle quali viene condotta, in condizioni che qui si ritengono di esistenza ed unicità, l’integrazione.
In tal modo, mentre l’azione a distanza richiede la conoscenza di tutte le sorgenti, la teoria di campo necessita della conoscenza delle
sole condizioni al contorno associabili alle sorgenti stesse.
Occorre allora mettere a punto gli strumenti di analisi. Si tratterà di grandezze del tipo f(P,t) Queste potranno essere rappresentative di campi scalari oppure saranno le componenti di vettori
Costituiranno le densità di causa (le forzanti) e le densità di effetto (le risposte) Trattandosi di teoria di campo, saranno espresse ( e dunque misurate) nel medesimo punto, come sempre, si dovranno associare ai valori attuali-locali le corrispondenti rapidità di variazione. Trattandosi di teoria di campo, tali rapidità andranno intese sia in senso spaziale che temporale.
Per le derivate temporali dn/dtn niente di nuovo. Basterà solo ricordare che esse sono associate alla freccia del tempo, per cui, se, n è pari, esse rappresentano fenomeni conservativi, mentre se è dispari sono associate a fenomeni dissipativi.
Per le derivate spaziali la cosa è un po’ più complessa, ma neanche tanto… Converrà innanzitutto calcolare il gradus, il passo per antonomasia, la direzione di massima variazione spaziale
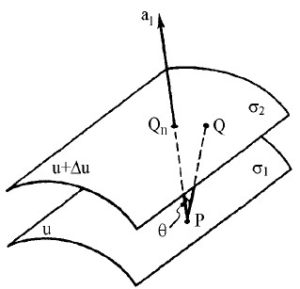
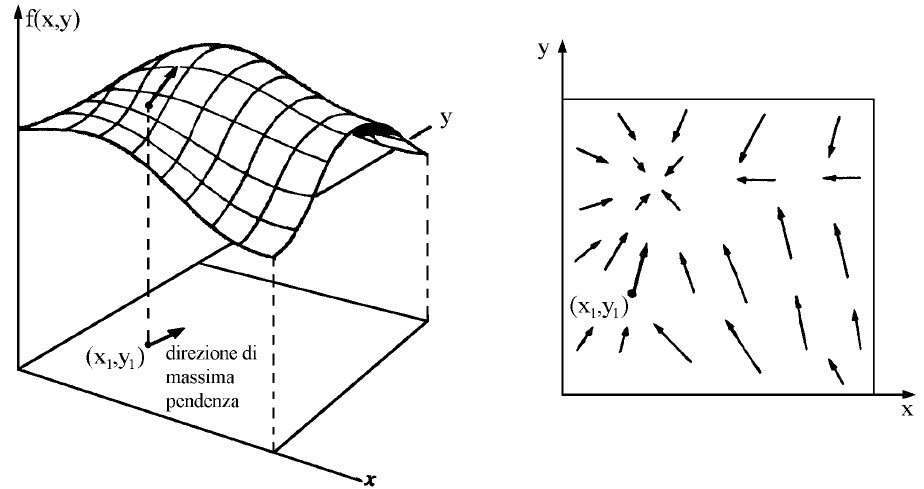
Ma non basta: occorrono anche le densità di sorgente La prima è una densità volumetrica scalare, la divergenza:
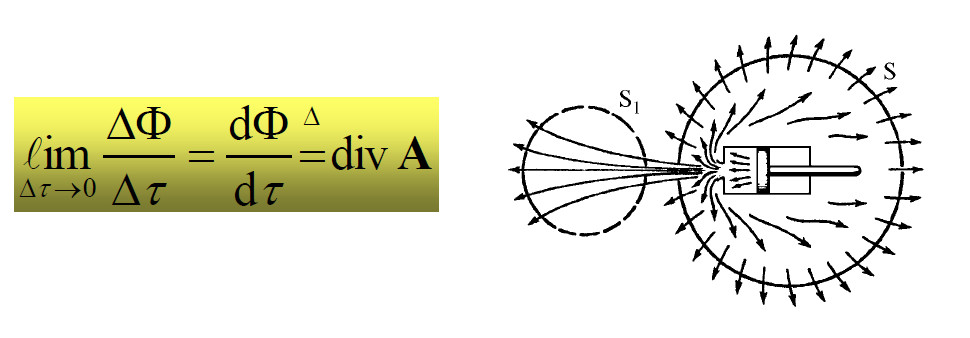
L’altra, compendiosa della “viscosità del mezzo”, è una densità vettoriale areolare di vortice: il rotore
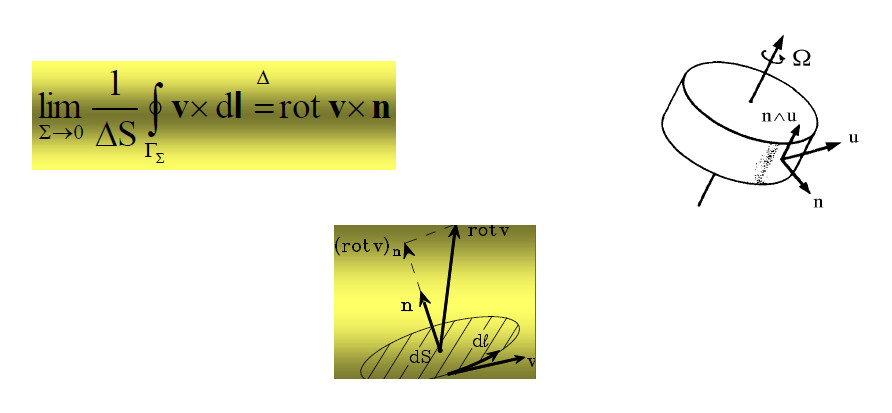
Occorre infine tener conto dell’elasticità del mezzo Maxwell denominò lo scalare
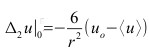
concentrazione volumetrica della grandezza u.
Il resto lo avrebbe fatto il teorema di Helmholtz Un teorema terribile, che noi possiamo presentare solo in modo elementare ed intuitivo
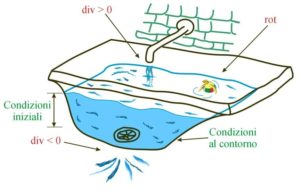
Un campo vero è una funzione matematica che si adopera per evitare l’idea di azione a distanza. R. Feymann Le equazioni di campo

Le equazioni di Maxwell rientrano in tale chiave di lettura ed in tale criterio di classificazione
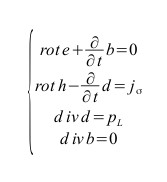
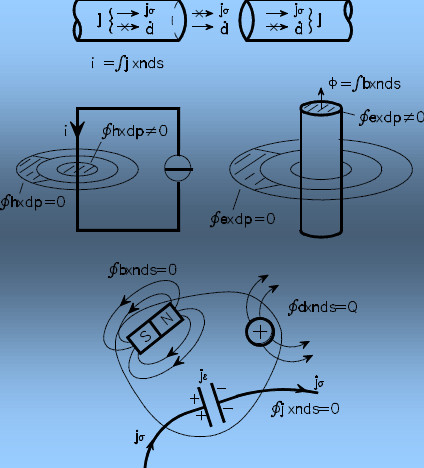
Il dato conoscitivo:
La classificazione è immutata rispetto al caso generale.
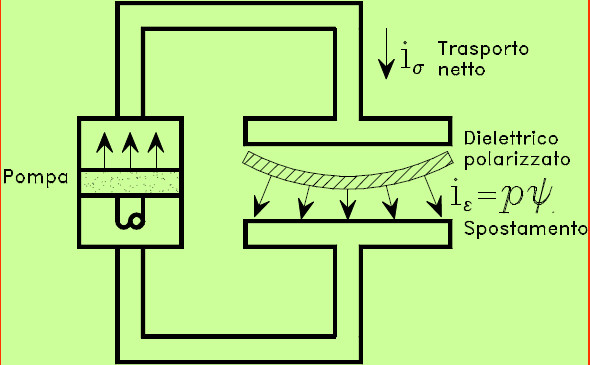
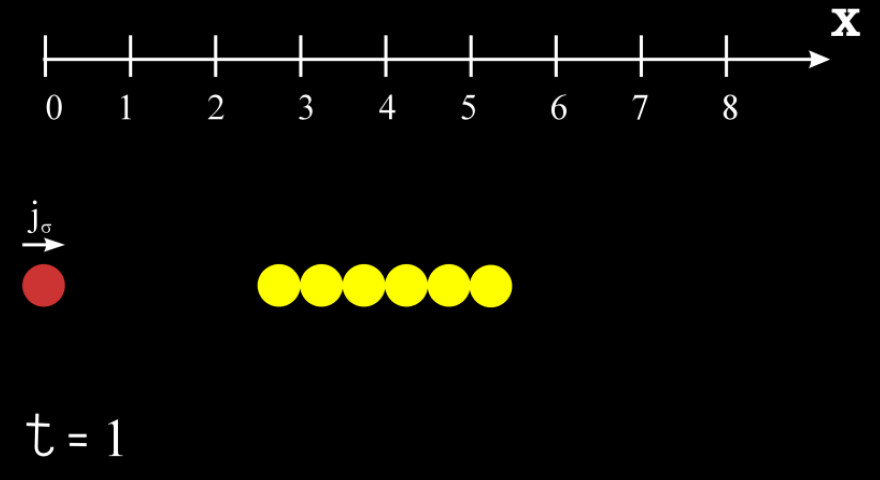
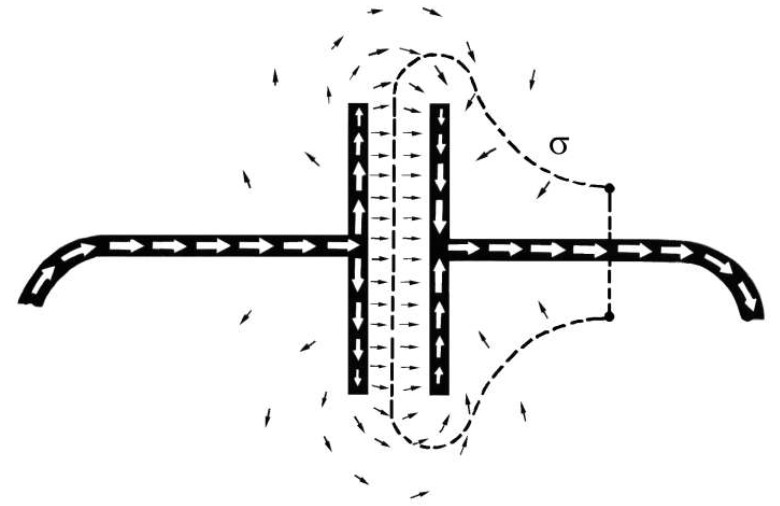
Tutto dipende dal ruolo delle due correnti:
- La corrente di conduzione nei conduttori
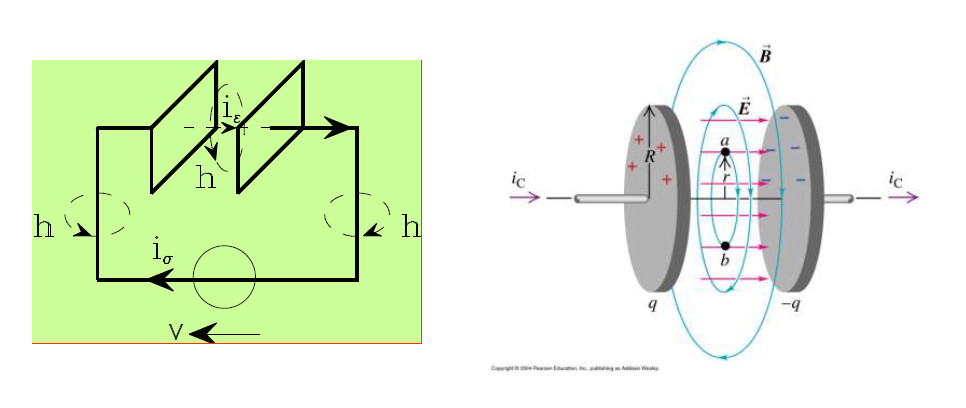
- La corrente di spostamento nei dielettrici.
Integrando vettorialmente per parti le equazioni di Maxwell, se ne ottiene l’integrale primo che costituisce la relazione di Poynting.