Luci, ombre

Luci, ombre ed “inflessioni maxwelliane”  sulla Teoria delle Reti Elettriche

• Schegge (frammentarie) di Storia della Scienza;
• Pozioni (robuste) di Fisica Matematica;
• Escursioni (ruspanti: da ingegnere) di “Epistemologia”

Relative:

• alla genesi del concetto di circuito elettrico;
• al suo significato intrinseco;
• al suo legame con la più generale e compendiosa Dynamical Theory.

Un incontro informale ed un insieme di spunti di riflessione

La partizione dell’Elettromagnetismo in

• Starkstromtechnik (correnti forti: potenza)
• Schwachstromtechnik (correnti deboli) ebbe, proprio in Italia, i due protagonisti per antonomasia

Con G. Ferraris, a Torino, l’ Elettromagnetismo quasi – stazionario avrebbe dato vita alla teoria scientifica del trasformatore (già esplicita negli scritti di Maxwell), al campo magnetico rotante e dunque alla II Rivoluzione Industriale (il continuatore sarebbe stato l’ingegnere russo- tedesco M. Osipovich Dolivo – Dobrovolsky);

Con A. Righi, a Bologna, l’Elettromagnetismo rapidamente variabile, partendo dalle precedenti sperimentazioni (Lodge, FitzGerald ed Hertz), avrebbe avuto uno sviluppo che avrebbe aperto l’ Era delle Telecomunicazioni.

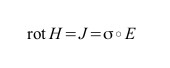
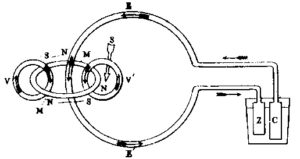
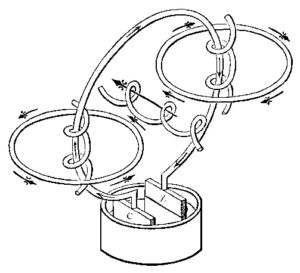
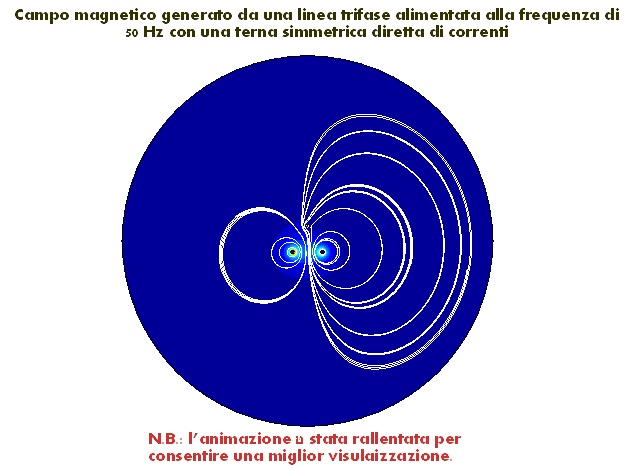
Campo magnetico rotante

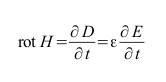
Induzione hertziana (onde elettromagnetiche)

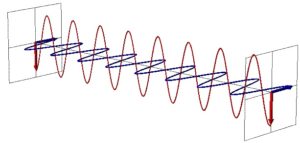
Non ci soffermeremo su questi aspetti preliminari, del resto ben noti; ci limiteremo invece, a proposito di Righi, a ricordare che in quei tempi si parlò di “Bologna delle radiazioni”.

Vi è poi un altro aspetto essenziale su cui occorre insistere con particolare evidenza, dato per acquisito – se ne parlerà nel dettaglio proprio tra qualche istante – che la teoria dei circuiti è il risultato di una formulazione approssimata della soluzione delle equazioni di Maxwell, occorre sottolineare che, se questa formalizzazione fu inizialmente elaborata nel 1928 da J.R. Carson presso i laboratori Bell, di fatto la versione più completa e rigorosa è, a tutt’oggi, quella elaborata, in modo del tutto indipendente, a Bologna, da Dario Graffi nel 1938.

Per quanto riguarda infine il ruolo giocato nello studio della scienza, dalla filosofia e dalla storia della scienza, non possiamo in alcun modo dimenticare l’insegnamento impartito, a Bologna, dal matematico, filosofo e storico della scienza Federigo Enriques e “l’esperienza incredibile” [che a tutt’oggi getta un’ombra inquietante sulla cultura italiana] della Rivista Scientia da lui fondata e diretta.

Limitiamoci a queste ombre veloci capaci di richiamare il ricordo e l’emozione per quelle vicende e per la grandezza di quell’Uomo.

Non stupitevi se mi vedete occuparmi di storia e magari di filosofia: questa non è che l’altra faccia dell’onesto lavoro dello scienziato. Una visione dinamica della scienza porta naturalmente nel terreno della storia.

Partiamo dunque con la Teoria delle Reti Elettriche. Domandiamoci che cosa, dal punto di vista concettuale e metodologico, tale approccio esprima e poniamo in luce, ove eventualmente esistano, le “incongruenze” implicite in tale chiave di lettura.

Poiché intendiamo porre in luce i legami tra le due chiavi di lettura, richiamiamo in via preliminare ed in forma separata i due distinti approcci:

• L’analisi campistica di Maxwell;
• L’analisi circuitale.

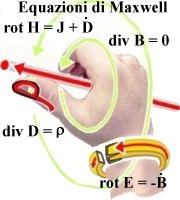
Equazioni di Maxwell

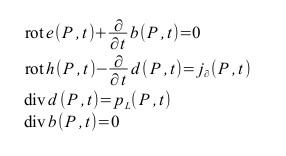
Vi si potrebbe ritrovare il Teorema di Helmholtz

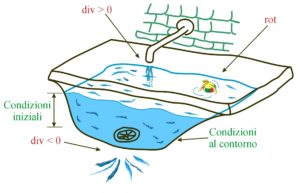
Che cosa se ne può dire?

Si percepisce ormai l’unificazione:

Regime	Legge ai rotori	equazione d’onda	equazione	fenomeno
t >> T		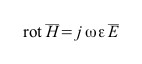	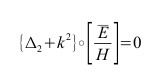iperbolica di Helmholtz	propagativo
t << T		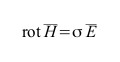	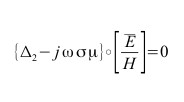parabolica di Fourier	diffusivo

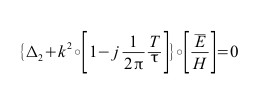
Con un integrale primo (relazione di Poynting)

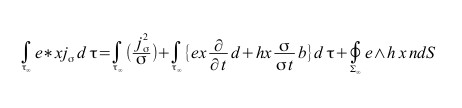integrale primo delle equazioni di Maxwell: la relazione di Poynting

Con un’equazione inomogenea d’onda (corrispondente alla condizione di Lorentz)

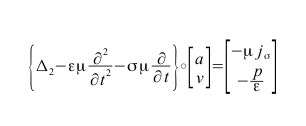
Il cui integrale è espresso dai seguenti potenziali ritardati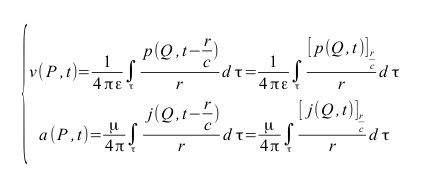
Il cui sviluppo in serie è sorprendente:

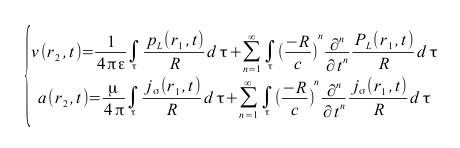
Solo il primo addendo è dunque un potenziale attuale (propagantesi in quanto tale con celerità infinita):

gli altri, di natura correttiva, sono potenziali ritardati che viaggiano a celerità finita!

Nel caso di regime sinusoidale, avvalendosi del metodo degli esponenziali complessi, si ha:

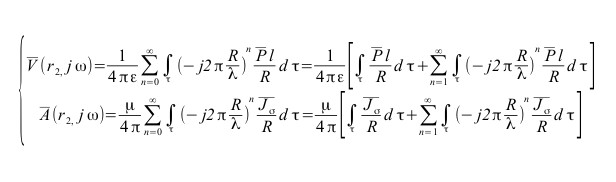In tali ipotesi, se:

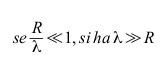
allora, troncando lo sviluppo in serie di potenze, si può adottare l’approssimazione di primo ordine così sintetizzata:

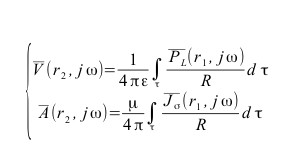
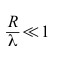cioè nell’ipotesi di approssimazione del primo ordine, l’effetto del ritardo dovuto alla velocità finita di propagazione può essere trascurato.

In tali condizioni, lo spazio ed il tempo nuovamente si disaccoppiano e lo spazio da fisico torna ad essere geometrico.

Quanto alla forma del potenziale, essa è dello stesso tipo del caso statico.0

In particolare, nel caso sinusoidale, se tali condizioni sono verificate, si dirà che il campo è lentamente variabile. Tramite tale notazione il campo sarà detto lentamente o rapidamente variabile in relazione alla distanza tra il potenziato ed il potenziante confrontata con la lunghezza d’onda.

Abbiamo preparato tutti i requisiti legati alla Dynamical Theory, che ci consentiranno di penetrare con consapevolezza l’essenza – ed i limiti – della teoria delle reti.

Una cosa è certa: poiché, lo si sa, la teoria delle reti (a costanti concentrate) è governata da equazioni differenziali ordinarie, il tempo nei vari punti è lo stesso: la teoria delle reti è dunque una teoria del primo ordine. Il che vuol dire che, contrariamente a quanto si è abituati a pensare, ben lungi dalla materialità costruttiva che la richiama e la materializza, che la rete elettrica non esiste.

Diciamocela tutta:

«Circuit theory is a mathematical method and it should not be confused with circuits. Empty space is neither a circuit nor a network».

S. Shelkunoff (1897-1992), Electromagnetic Fields, Blaisdell Publishing Company, New York, 1963.

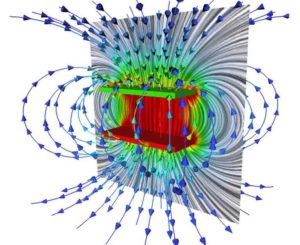
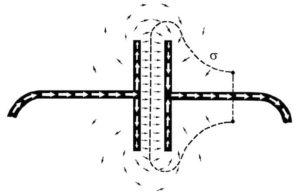
Insomma, pur essendo governato da equazioni dello stesso tipo di quelle della Meccanica Razionale (equazioni cardinali, attrito viscoso, elasticità, inerzia, etc.) il circuito non è introflesso, ma, con le sue linee di forza che si spingono verso l’esterno per cercare di lambire gli altri componenti, è estroflesso.

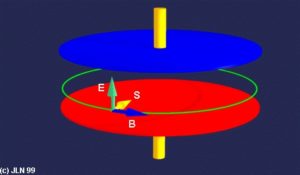
Ammesso che un insieme di apparecchiature di questo tipo, solo in ragione della propria materialità costruttiva, sia legittimamente denominabile circuito elettrico:

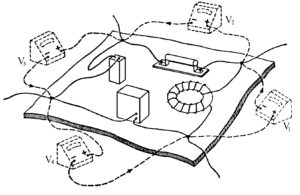Si deve pensare a configurazioni di questo tipo:

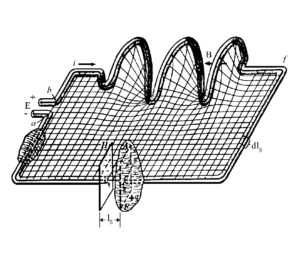
Dove lo spazio, compromesso con l’evento, va visto a priori compromesso con l’evento e dunque fisico:

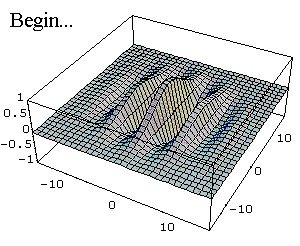
E dove solo a posteriori si potrà dire se sussistono le condizioni del primo ordine per le quali il campo si può lasciar rappresentare in modo “particellare” da una rete.

Ma vediamo l’essenza di una rete: riporta topologicamente alla Teoria dei Grafi e tipologicamente, a livello di algoritmo, alla Teoria deiSistemi. Diamo, all’interno di un approccio ipotetico – deduttivo, alcune nozioni

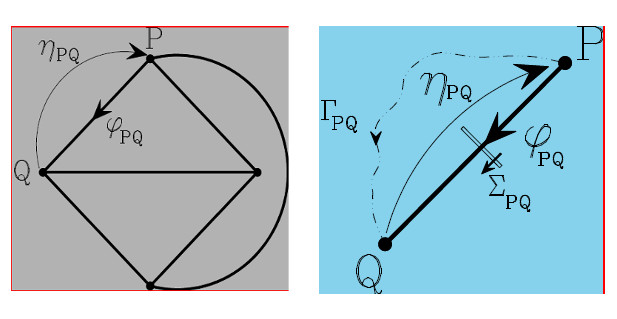
Trans – variabili (o grandezze – tra)univocamente associate ad una coppia ordinata di nodi.

Per – variabili (o grandezze attraverso)

univocamente associate ad un lato orientato (identificato ai suoi estremi dalla coppia ordinata di nodi PQ).

Per esse valgono poi, in termini di postulato, le due seguenti Equazioni Cardinali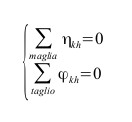

postulato delle maglie: la somma algebrica delle trans-variabili associate ad una qualunque maglia del grafo è nulla.

postulato degli insiemi di taglio: la somma algebrica delle per-variabili associate ad un qualunque insieme di taglio del grafo è nulla.

Il loro integrale temporale costituisce le corrispondenti grandezze estensive. Si ha dunque il seguente legame:

le grandezze

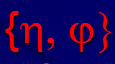
in tal modo definite vengono denominate intensive. Il loro integrale temporale costituisce le corrispondenti grandezze estensive.

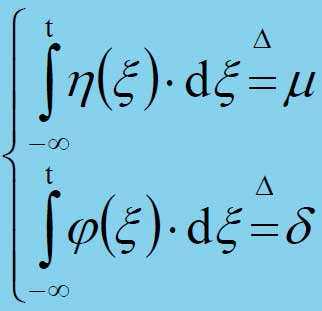
Le variabili estensive, secondo una terminologia che è tradizionale sia in
Termodinamica che in Teoria dei Sistemi, sono denominate variabili di stato.

Da cui in sintesi:

Costruite le matrici di incidenza ridotte di Poincarè, è immediato trovare le incognite tra ed attraverso e dimostrare su base topologica, la conservazione della “potenza”

 

Parlare di circuito elettrico vuol dire allora:

• Adagiare nello spazio un grafo elettrico;
• Adottare come nodi i “morsetti di circuito” oggetto di interesse;
• Riferirsi alla carica elettrica libera e con essa definire le grandezze concrete tra ed attraverso tensione (ddp) e corrente (di conduzione).

 

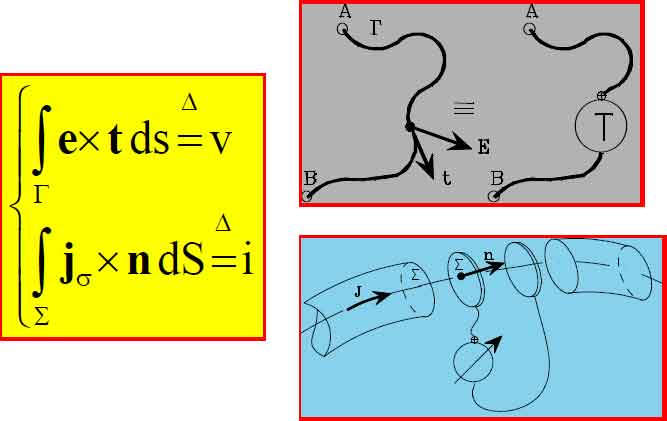
Con “incertezze” che sono immediatamente visualizzabili:

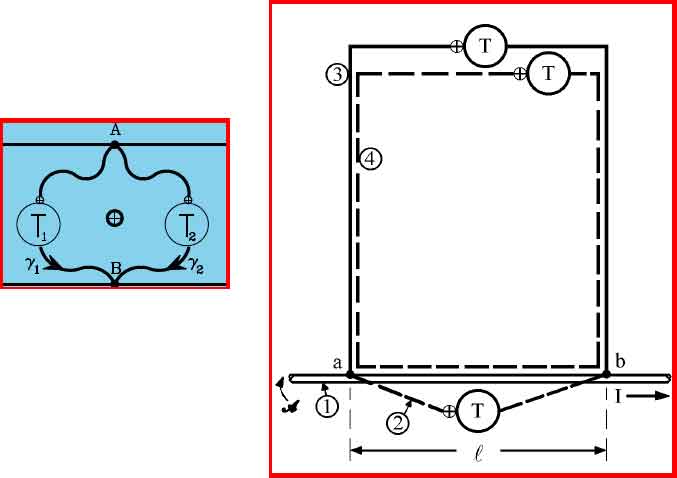
E che trovano riscontro con quella nozione tipologica di “grafo di componente” nella quale si ritrova la nozione di bipolo. Per brevità, ma in modo incisivo, lavoriamo per immagini:

 

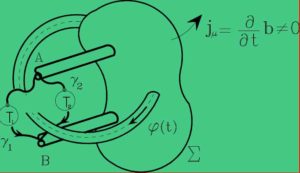
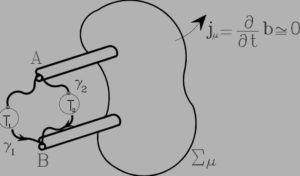
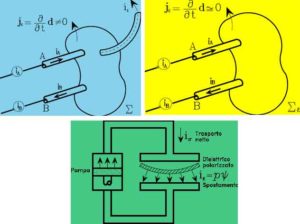
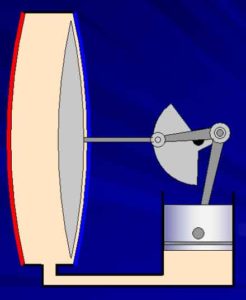
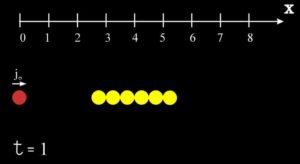
Ma restando sempre accuratamente all’esterno della frontiera elettromagnetica: dunque con un approccio agnostico.

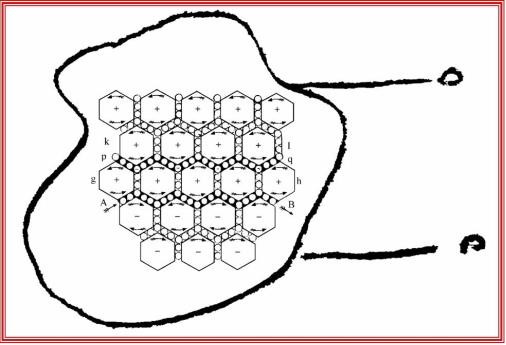
E dunque non puntando, a partire da grandezze cocrete, sulla equivalenza agli effetti interni.

È il caso del mutuo induttore

 

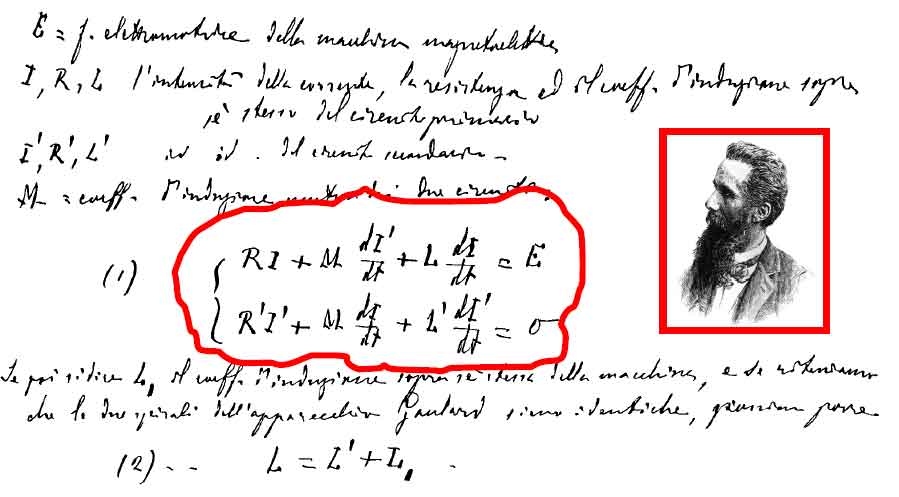
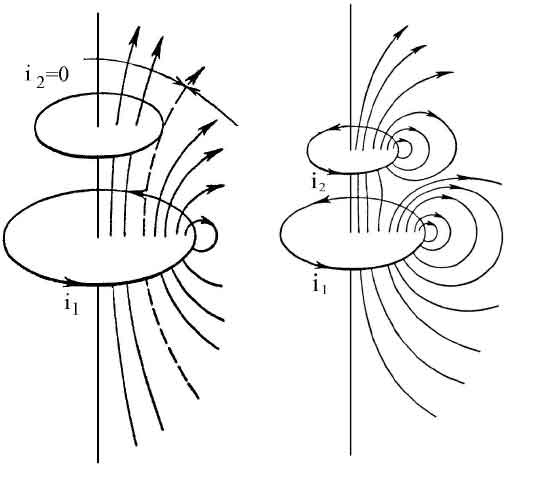
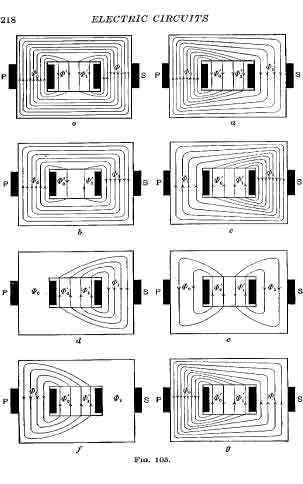
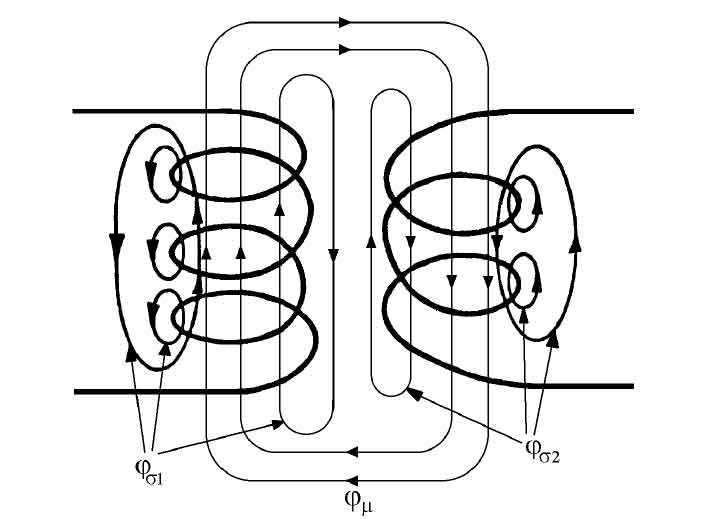
Avendo ben presente il “postulato vj degli ingegneri” e riformulando corrispondentemente la relazione di Poynting secondo Slep
ian.

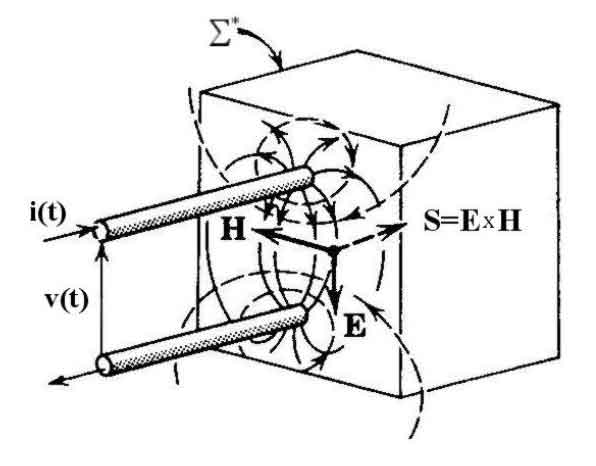
teoria delle reti elettriche

Infine con Poincaré, le grosse difficoltà appariranno proprio in occasione, guarda caso, dell’experimentum crucis di Hertz.

Hertz sperimenta con alte frequenze ma, per calcolare la frequenza naturale con la formula di Kelvin, commette l’errore di avvalersi delle formule
stazionarie di Neumann.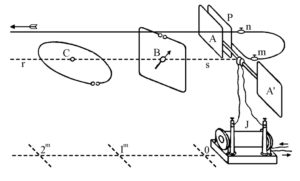

A svelare l’enigma inatteso (regime quasi-stazionario) dell’approccio circuitale saranno le “percezioni” contenute in una lettera inviata da di Heaviside ad Hertz.

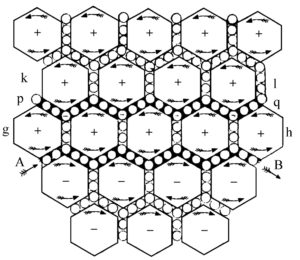
La conclusione arriva nel 1938, con l’analisi tensoriale delle reti di Gabriel Kron, con le sue reti elettriche equivalenti delle Equazioni di Maxwell:

Nelle quali si ritrova il pensiero di Levi-Civita.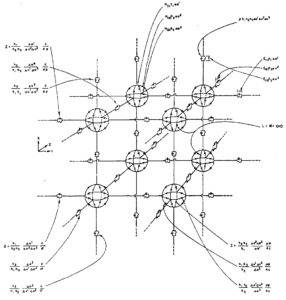

Noi siamo i musicanti
Siamo i sognatori di sogni
Erranti per solitari marosi E seduti lungo corsi d’acqua desolati;
Alla luce pallida della luna
Noi perdiamo il mondo,
Noi abbandoniamo il mondo; Eppure sembra che siamo noi a muovere,
Ad agitare il mondo per sempre.