Sulle equazioni di Maxwell

Il tema, lo ricordiamo, è quello implicito nella seguente transizione:

Lo scienziato: Maxwell	L’inventore ingegnere: Steinmetz	Lo scienziato inventore: Ferraris

• Maxwell ha studiato Mossotti;
• Ferraris ha studiato Maxwell;
• Steinmetz ha studiato Maxwell, Ferraris e Kittler;
• Quando giunge a New York, si fa inviare dal padre, in Germania, una copia del Treatise ed una copia del Kittler;
• Per anni, il suo alter ego, Ernst Berg, farà la spola tra New York e Londra per consultarsi con Heaviside.

Urge a questo punto richiamare senz’altro le equazioni di Maxwell ed esplicitarne il senso metodologico.

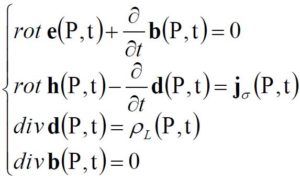Vediamone l’anatomia:

Nihil agit in distans nisi prius agit in medium.

Le equazioni di Maxwell sono la quint’essenza dell’azione a contatto (quel “mediante ed attraverso” faradiano che sostituisce il semplicistico “attraverso” newtoniano).

Fissiamo le idee sull’azione a distanza per eccellenza: l’interazione gravitazionale newtoniana e vediamone l’anatomia.

 

 

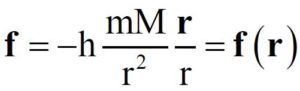
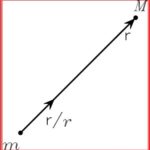
L’anatomia della equazione:

• Il campo, funzione di r/r, è centrale (e dunque conservativo);
• I due attori del fenomeno sono remoti ed usano la stessa variabile tempo;
• Ciò significa che i segnali che essi si scambiano si propagano con celerità infinita;
• Lo spazio, ridotto al rango di solo contenitore di corpi, è dunque puramente geometrico • È dunque del tutto estraneo all’evento

E se il segnale decidesse di viaggiare a velocità finita?

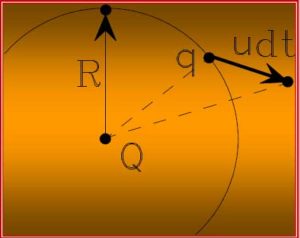
L’eventuale idea di una velocità finita nel modello è inaccettabile: con essa salterebbe infatti il terzo principio della Dinamica;

Le equazioni di Maxwell aderiscono invece ad una suggestione neocartesiana. Nella quale, in qualche modo, adeguatamente matematizzati, ritornano i tourbillones.

Ricordiamo al riguardo il vortice molecolare maxwelliano, il modello con il quale, meccanicisticamente, egli modellizza quel vincolo anolonomo che è l’etere luminifero.

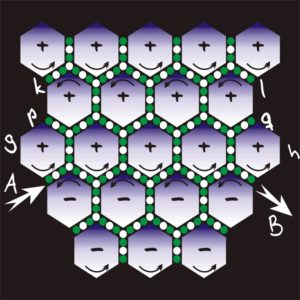
Come sarà mostrato tra poco, nelle equazioni di Maxwell, come già nei tourbillones di Descartes, il medium, compromesso con l’evento, è il protagonista del fenomeno e le masse sono delle semplici lacune. Causa ed effetto (all’interno di un’equazione differenziale alle derivate parziali [Faraday seppe vedere materia dove i matematici avevano visto solo spazio]) non sono più remoti ma sono invece espressi nello stesso punto e nel medesimo istante. Le linee di forza, fisiche e non solo puramente matematiche, si incurvano al procedere dell’evento; Il che vuol dire che, iterando, dal punto P al punto P+dP, dall’istante t all’istante t+dt, si percorre tutto lo spazio – tempo e si giunge ai “bordi”, dove, tra tutte le soluzioni possibili, viene scelta quella che rispetta le condizioni iniziali, cioè la storia passata, e le condizioni al contorno, cioè il mondo esterno.

Ma quali sono gli strumenti con i quali, matematicamente, si esprimono le modalità con le quali la Natura trasmette, nella materia, i proprio poteri da punto a punto, per contiguità e continuità,

Cominciamo col ricordare il formalismo dei fenomeni ondosi:

Le equazioni sono quelle ben note di d’Alembert:

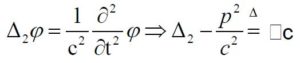
Si noti la presenza del laplaciano, dell’operatore di Heaviside e del dalembertiano:

Più in generale si porrà:

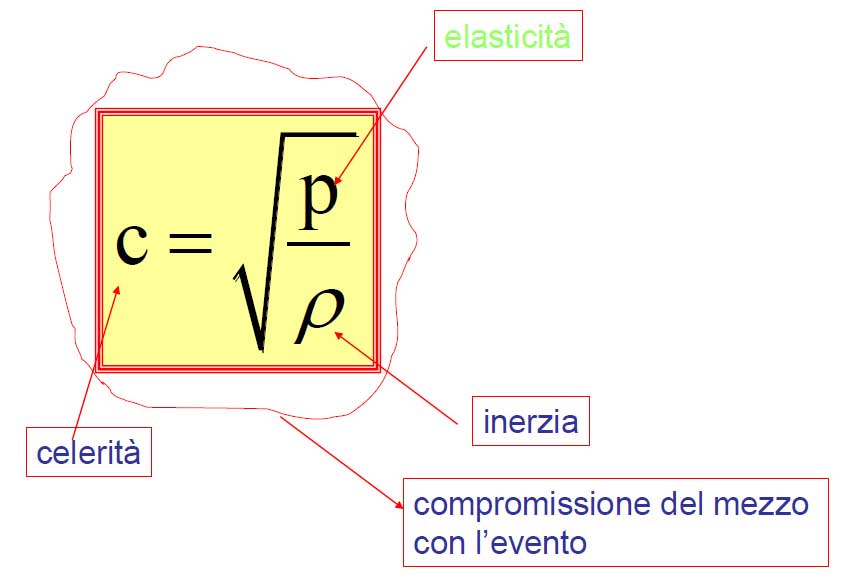
Un esempio significativo è quello della fune

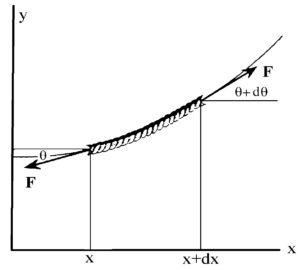
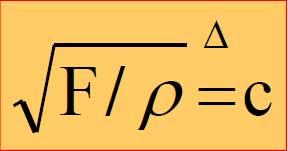
Le cose si complicano nel caso della linea elettrica

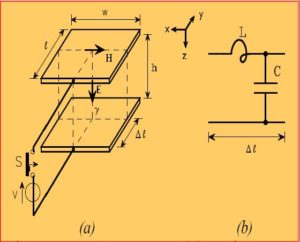
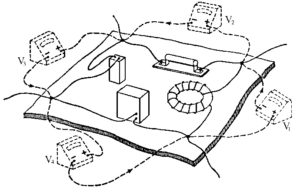
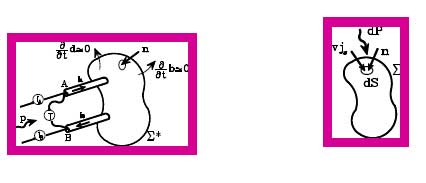
Anatomia del fenomeno elettromagnetico propagativo in un doppio strato.

L’equazione è dello stesso tipo della fune e della sbarra:

 

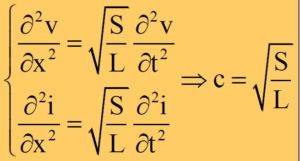
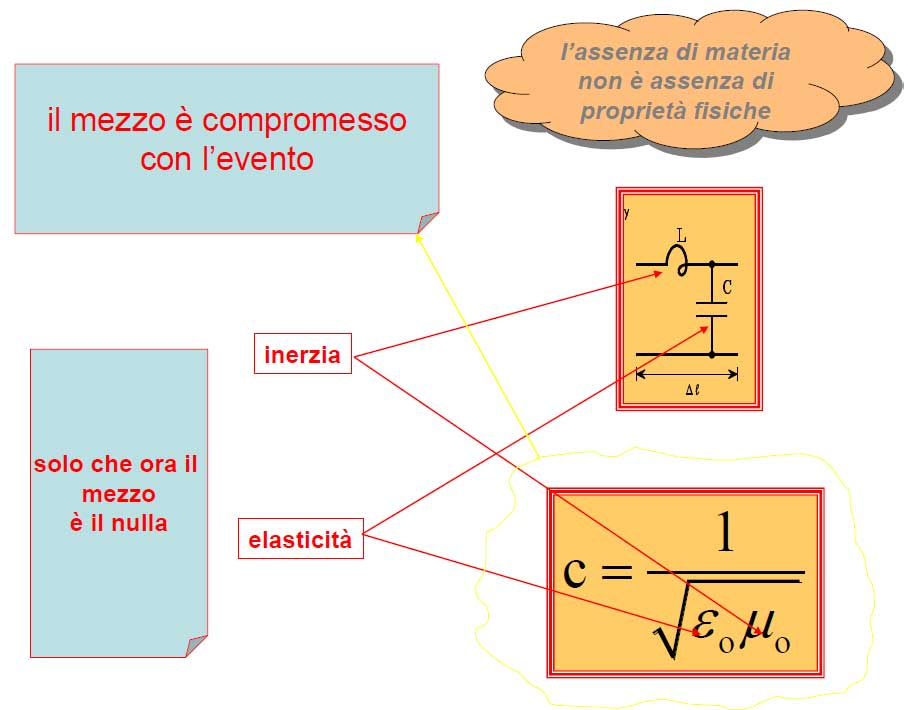
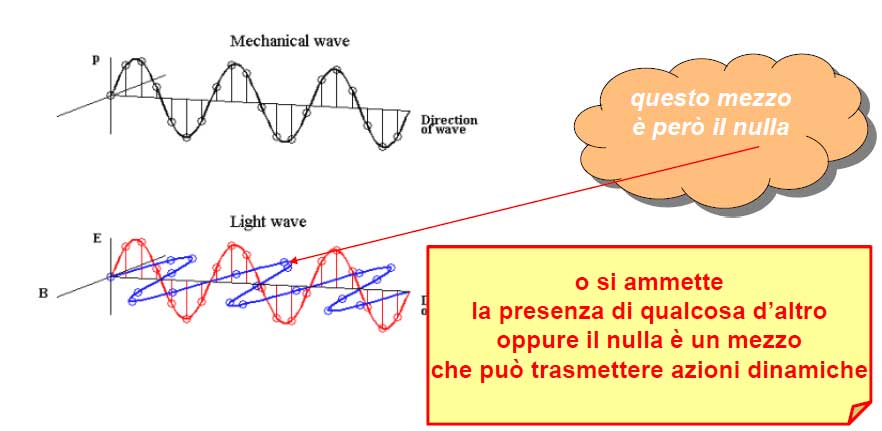
Tutto avviene come nel caso meccanico: il conduttore guida fenomeni energetici che avvengono nel mezzo Mentre la materia agisce laddove esiste, l’energia “agisce” laddove si accumula.

• Essa può accumularsi anche nel nulla
• Come sostanza imponderabile è dunque meglio del calorico, dell’elettrico e del magnetico.

Come si fa a mettere a punto il formalismo analitico ed applicarlo alle funzioni vettoriali di punto e del tempo v(P,t)?

Per il tempo, la rapidità di accrescimento è espressa della derivate temporali; quelle di indice pari, indipendenti dalla freccia del tempo, esprimono fenomeni conservativi, quelle di indice dispari, dipendenti dalla freccia del tempo, esprimono fenomeni dissipativi.

Poi si hanno, e qui le scelte possibili sono molte, le derivate spaziali. Converrà innanzitutto calcolare il gradus, il passo per antonomasia, la direzione di massima variazione spaziale

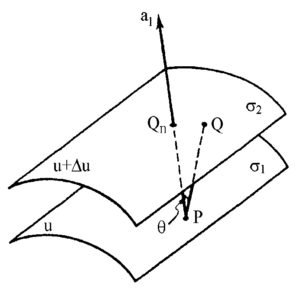
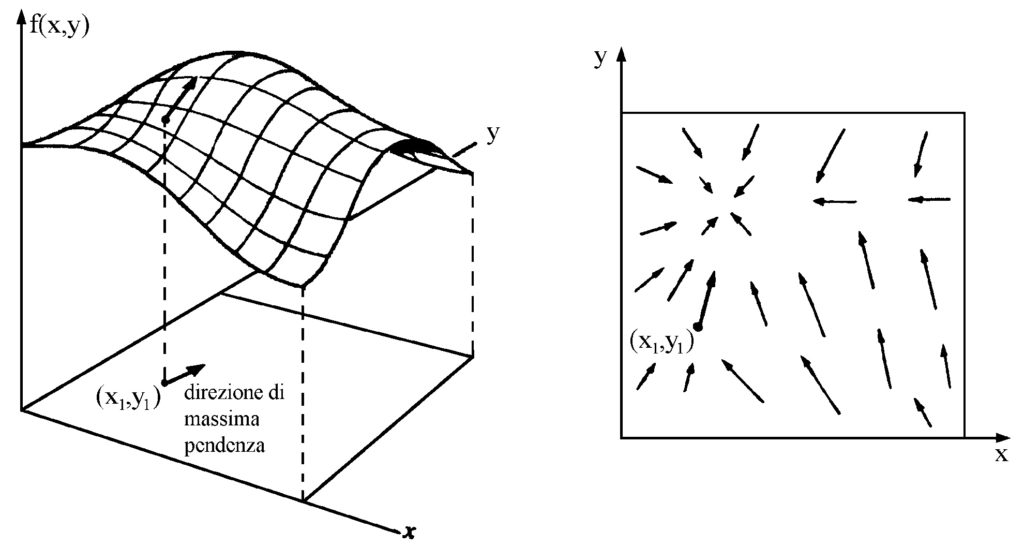
Ma non basta: occorrono anche le densità di sorgente La prima è una densità volumetrica scalare, la divergenza:

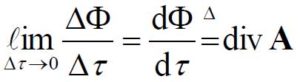
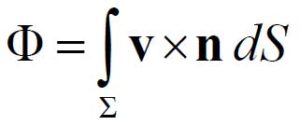
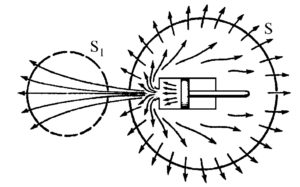
L’altra, compendiosa della “viscosità del mezzo”, è una densità vettoriale areolare di vortice: il rotore lim

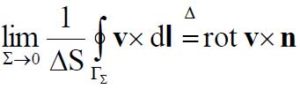
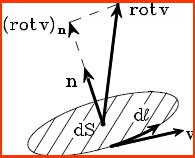
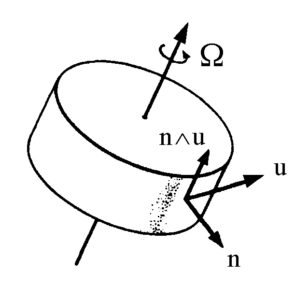
Occorre infine tener conto dell’elasticità del mezzo, Maxwell denominò lo scalare

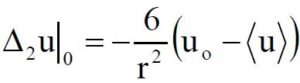
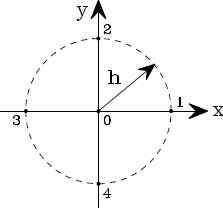
concentrazione volumetrica della grandezza u.

Il tutto nella consapevolezza del Teorema di Helmholtz sul calcolo vettoriale

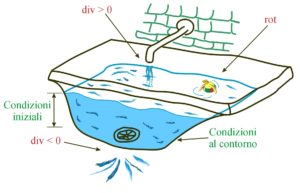
E nel fatto che le EDM, avendo al primo membro come incognite non solo il rotore e la divergenza ma anche i termini dalembertiani espressione del displacement, non godono in generale di questo privilegio.

Vediamone il dato fenomenologico:

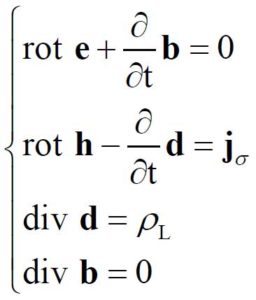
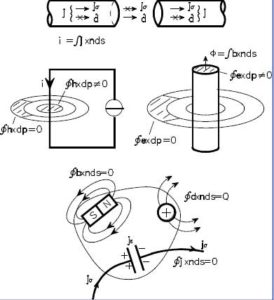
E il dato conoscitivo:

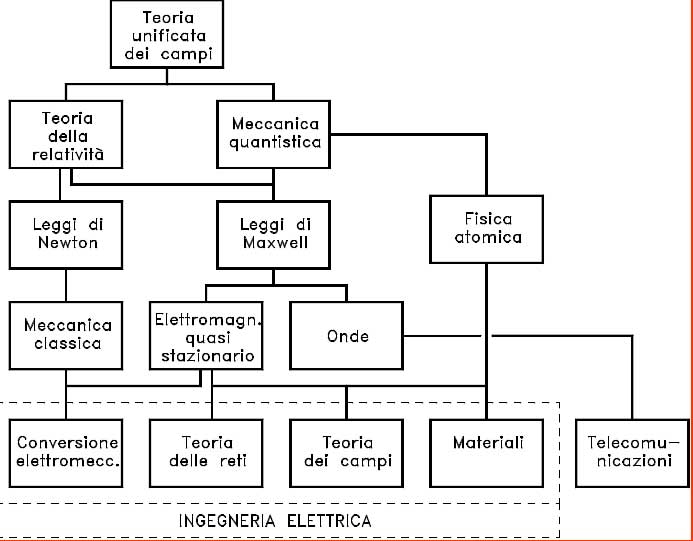
Tutto dipende dal ruolo delle due correnti:

• La corrente di conduzione nei conduttori
• La corrente di spostamento nei dielettrici

La corrente di conduzione: un trasporto netto. L’enigma della corrente di spostamento:

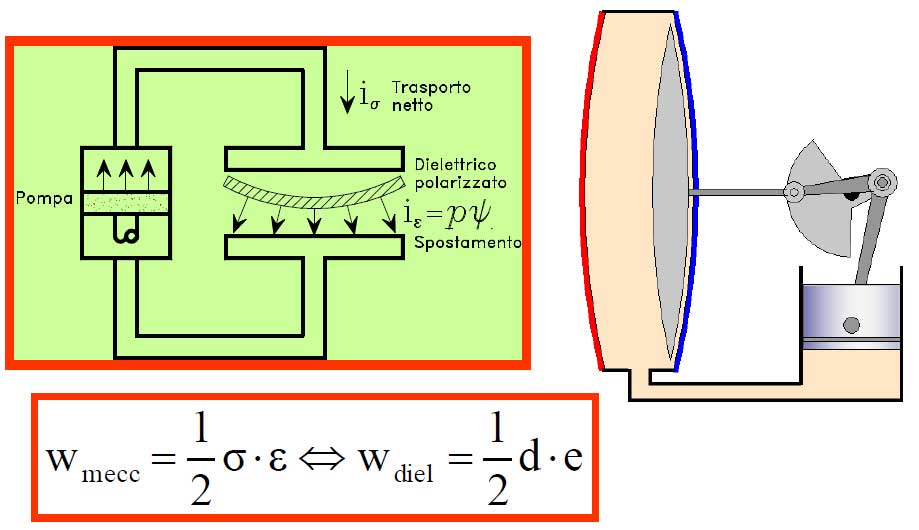
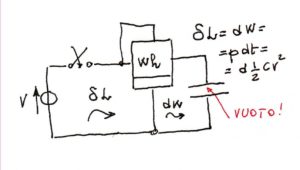
sempre in odore di meccanicismo

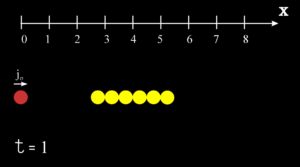
Una semplice prosecuzione della corrente di conduzione

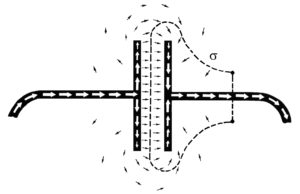
dovuta al fatto che il campo magnetico è prodotto solo da correnti chiuse

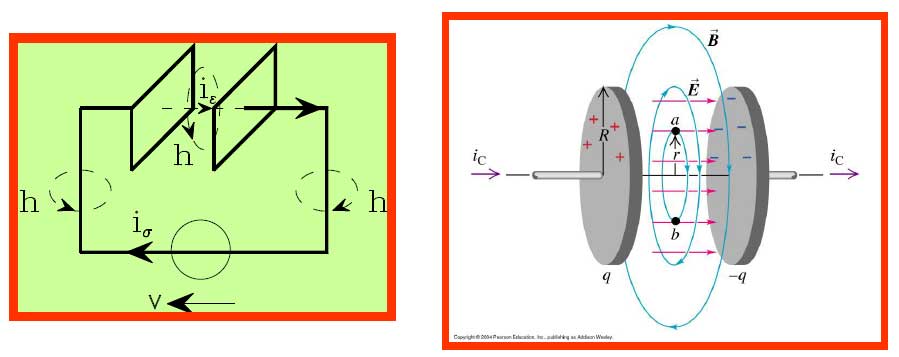
E dunque che la corrente di spostamento dielettrico deve essere indistinguibile da quella di conduzione nel produrre campo magnetico.

In modo analogo c’è la legge di Faraday

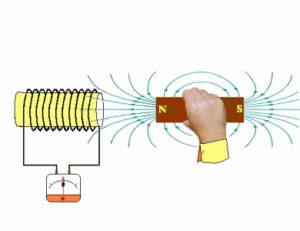
E ci sono le leggi ai pozzi ed alle sorgenti:

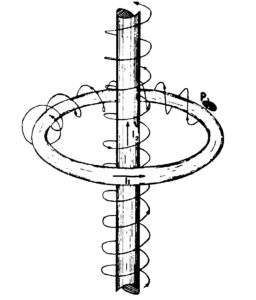
Con i corrispondenti strumenti integratori:

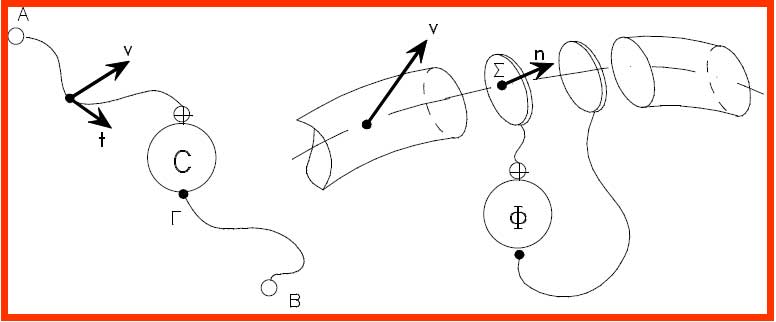
Infine si hanno le relazioni integrali:

L’integrale primo dell’energia Integrando vettorialmente per parti le equazioni di Maxwell, se ne ottiene l’integrale primo che costituisce la relazione di Poynting

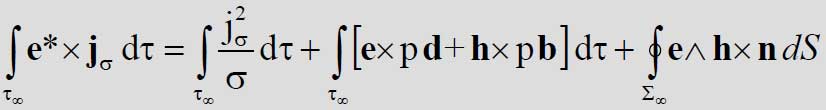
Legate al campo elettrico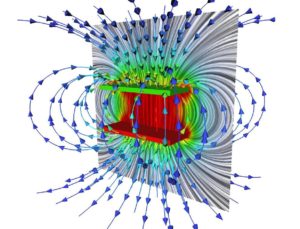

ed alle linee di forza del campo magnetico:

In quello che risulta essere il campo elettromagnetico

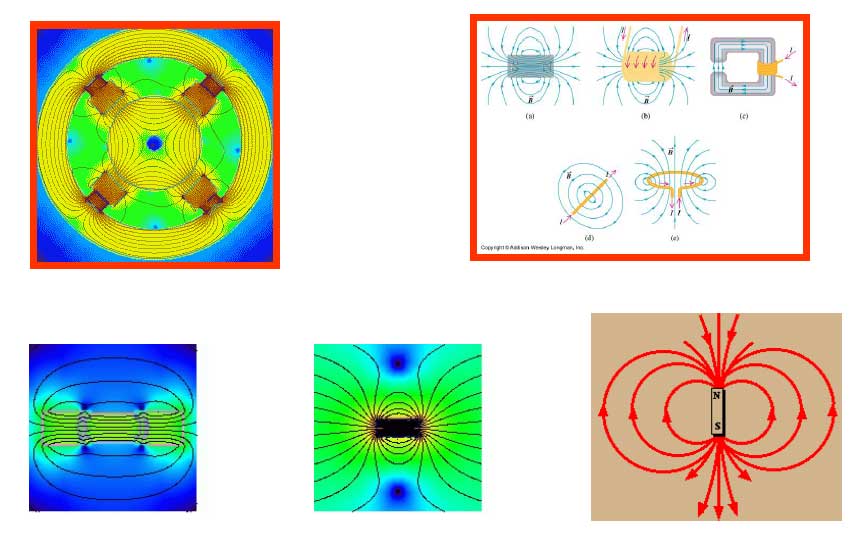
Ci sono poi i fenomeni ondosi:

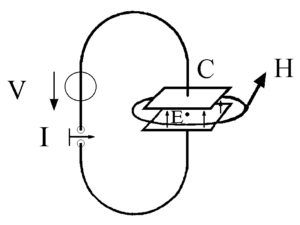
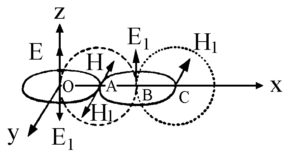
Al riguardo, l’elaborazione delle equazioni di Maxwell dà luogo ad equazioni d’onda del tipo seguente:

 

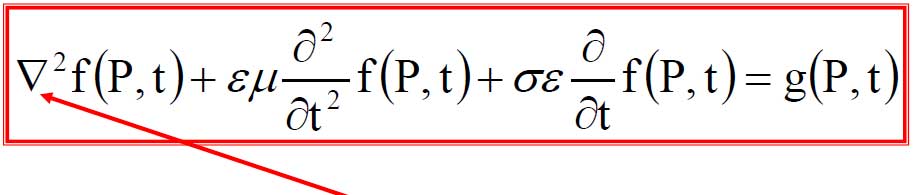
La presenza del laplaciano, espressione – con Maxwell – della concentrazione volumetrica nell’intorno del punto, segnala il coinvolgimento del mezzo con l’evento: lo spazio non è geometrico, ma fisico: In presenza dell’evento le linee di forza si incurvano, si tendono e si torcono.

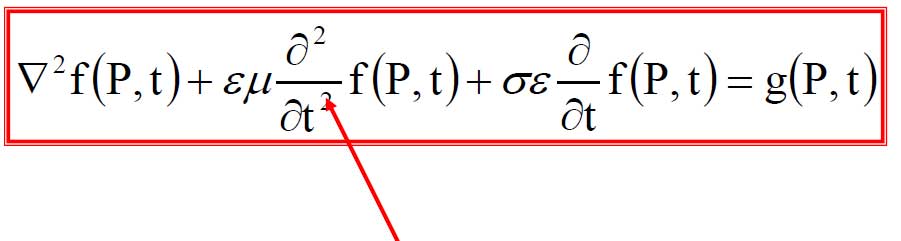
La derivata temporale seconda della variabile lagrangiana f, non dipendendo dalla freccia del tempo, rappresenta fenomeni conservativi;

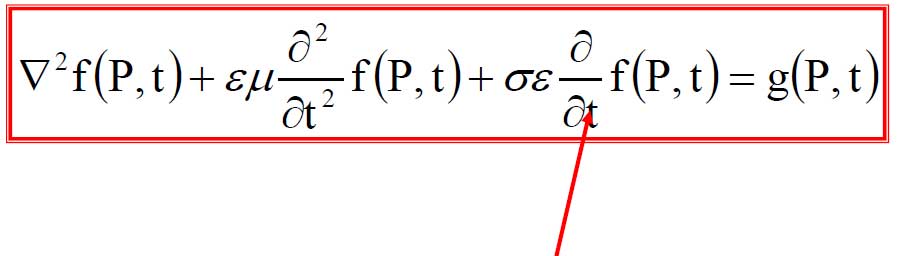
La derivata temporale prima, invertendosi con la freccia del tempo, rappresenta invece fenomeni dissipativi;

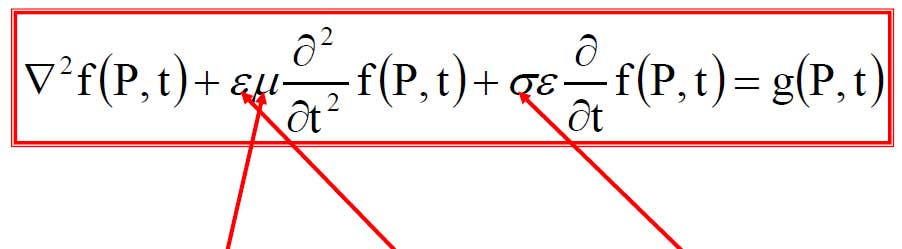
Lo spazio è dinamicamente coinvolto in ragione della sua inerzia, della sua elasticità e della sua viscosità.

Un campo vero è una funzione matematica che si adopera per evitare l’idea di azione a distanza.
R. Feymann

Facciamone la classificazione:

Azione per contatto	Azione a distanza	Azione per pseudocontatto
Teoria pura di campo	Teoria newtoniana	Teoria di campo
Celerità finita	Celerità infinita	Celerità infinita
Leggi locali di tipo differenziale	Leggi globali di tipo integrale	Leggi locali di tipo differenziale
Compromissione mezzo-evento	Assenza di compromissione	Assenza di compromissione

 

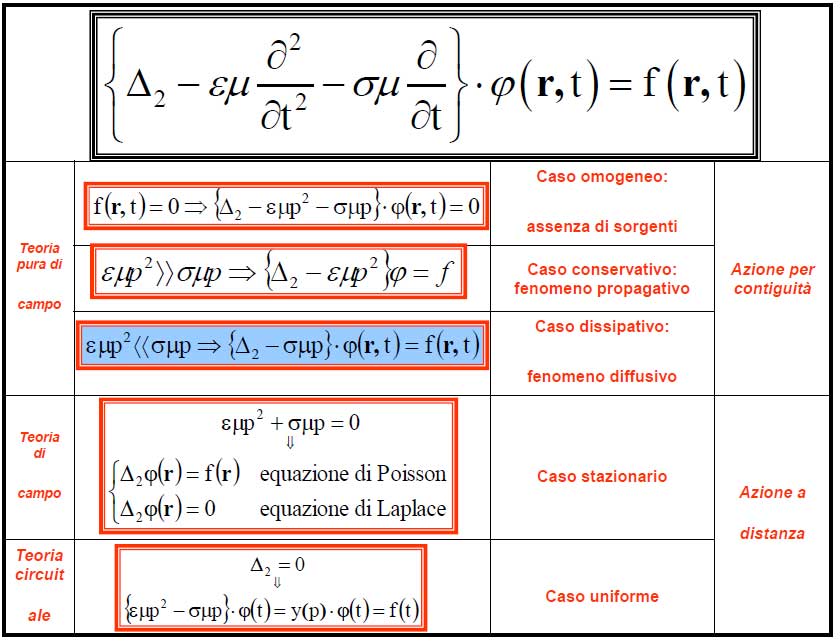
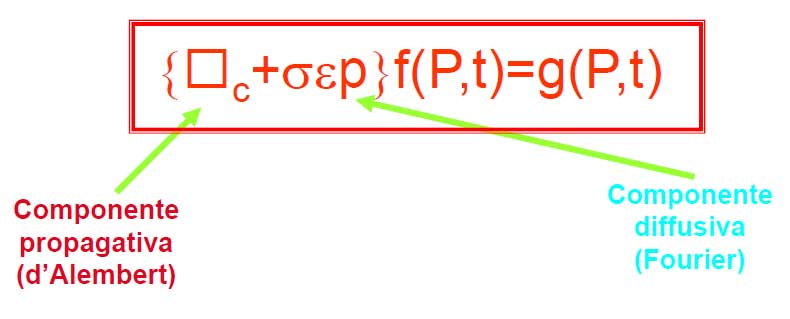
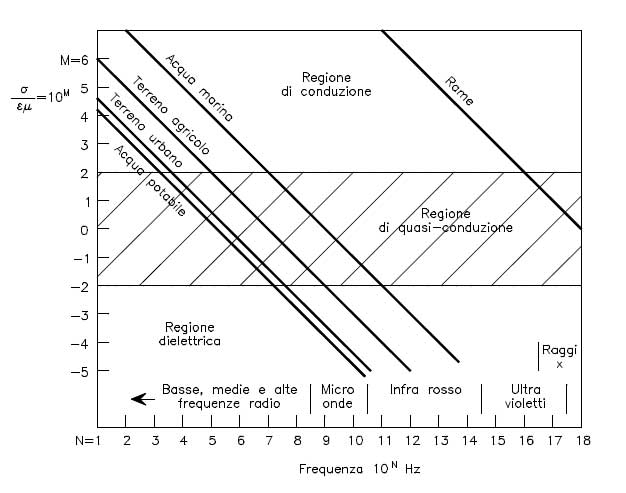
• Maggiori indicazioni, in merito alla compromissione del mezzo con l’evento, si ottengono considerando l’onda monocromatica;
• Avvalendosi cioè del metodo degli esponenziali complessi;
• Con tali premesse, operando nel dominio del numero d’onda si ha:
• 

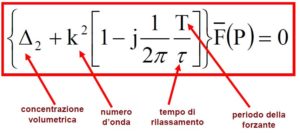
in ragione del rapporto T/t, le modalità di coinvolgimento del mezzo risultano le seguenti:

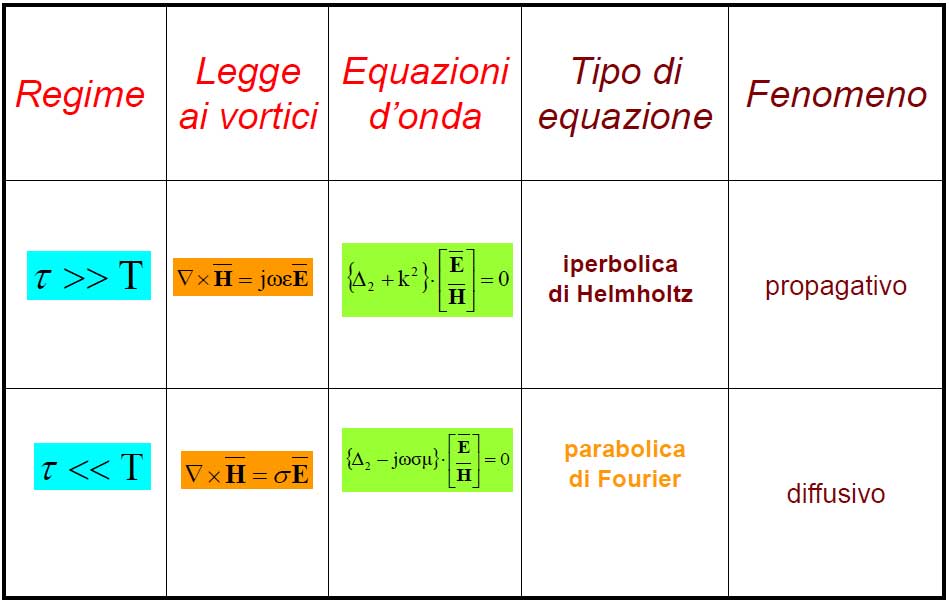
A conferma di come lo spazio sia fisico e non semplicisticamente geometrico come nell’azione newtoniana a distanza, i potenziali sono ritardati:

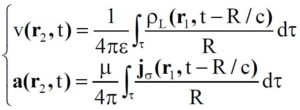
La lettura newtoniana a distanza corrisponde dunque ad una teoria del primo ordine:

Si formalizza dunque il regime quasi-stazionario:

Vediamo qualche ricaduta applicativa:

Va ricordato al riguardo che la teoria del mutuo induttore, l’elemento portante della conversione elettromeccanica, si deve a Maxwell, il quale, nel 1864, la pubblicò sulla sua Dynamical Theory.

A parte il simbolismo, l’approccio lagrangiano adottato da Maxwell è già quello attuale. Il suo approccio, basato sul metodo delle induttanze, punta sull’impiego della sovrapposizione delle cause e degli effetti e, partizionando l’impulso di tensione in auto e mutuo flusso, può conseguire la sola equivalenza agli effetti esterni.

Nei riguardi delle Tecnologie Elettriche, il suo contributo passa però del tutto inosservato. È Galileo Ferraris a riprenderlo nel momento in cui, per la Torino – Lanzo, elabora la prima teoria scientifica del trasformatore;

Il simbolismo da lui adottato diviene quello attuale.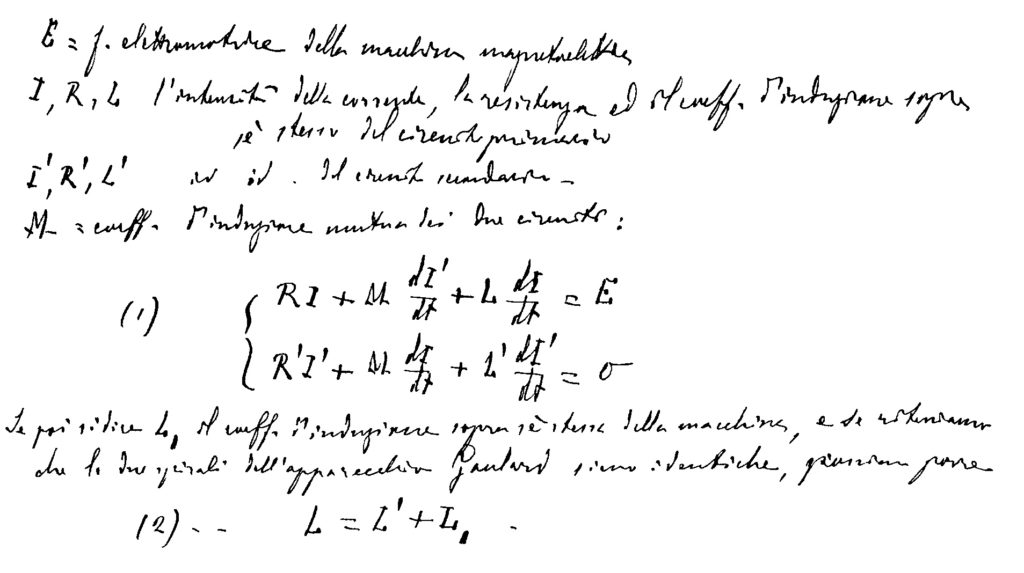

Ma Ferraris sferra anche il primo colpo alle perdite per isteresi. Da buon fisico matematico le mette in conto in assenza di non linearità conteggiandone l’effetto con un ritardo equivalente.

Tuttavia i risultati iniziali sono giudicati non soddisfacenti in quanto da più parti si ritiene che:

electrical engineering was born yesterday and had no long-standing tradition, no professional culture

Al riguardo Steinmetz osserva inoltre che:

The theory of the transformer described a device that does not exist in practise, but merely haunts as a phantom transformers the text-books and mathematical treatise on transformers

Ma poi rincara la dose:

Most theories of the induction motor were written only by theorist who never constructed a motor themselves and who have never seen a motor aken apart

Phantom transmission lines circuit of uniformly distributed capacity and inductance was very different from the circuit existing in practice

Scienza e Tecnica si attestano dunque su due posizioni opposte

Lo Scienziato J.C. Maxwell	Il Fisico Matematico M. Pupin	Il Fisico Matematico che diventa Ingegnere C.P. Steinmtez

Vedendo giustamente in Maxwell il padre sia delle teoria dei campi che della teoria dei circuiti, Pupin giunge ad affermare che:

Attemps of ordinary mortals to do better than Maxwell did must discouraged. Let us follow Maxwell as long as we can, then, when someone is born who is more profound than Maxwell, we will bow him

Ma non basta: occorre che i fisici matematici di alto profilo che decidono di diventare ingegneri sappiano aggiungere alla sua teoria la concretezza richiesta dalle applicazioni, in quanto:

Un’ equazione fisica è una relazione matematica tra grandezze misurabili • Se all’analisi può anche bastare (in prima lettura) l’ equivalenza agli effetti esterni (su grandezze globali), alla sintesi risulta indispensabile l’equivalenza agli effetti interni (su grandezze specifiche locali)

Un matematico infinitamente abile, integrando le equazioni di Maxwell, potrebbe dedurre ogni fenomeno elettromagnetico macroscopico.

Ma questo è vero solo in modesta misura in quanto:

• Davanti alle non linearità il matematico infintamente abile esiste solo sulla carta perché la matematica stessa non risulta infinitamente abile;
• Le equazioni di Maxwell dicono tutto perché astutamente prendono le distanze;
• A far la differenza, di volta in volta, sono le condizioni al contorno e i legami costitutivi, cioè il “braccio secolare” dell’Elettromagnetismo;
• E lì il gioco, duramente, passa all’Ingegneria… • Alla sua “astuzia” ed al suo potere evocativo.

 

La storia e l’episteme dell’Ingegneria Elettromagnetica sono un palleggio tra queste due realtà:

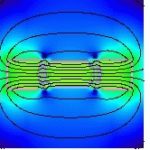Correnti forti: potenza	Correnti deboli: segnale

Le critiche e le difficoltà investono dunque sia la potenza che il segnale. Nel caso della potenza il problema è risolto da Steinmetz. Mantenendo l’approccio di Maxwell, legato, con equivalenza ai soli effetti esterni, al flusso medio per spira:

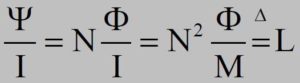
È la nascita postmaxwelliana dell’Elettrotecnica Teorica.

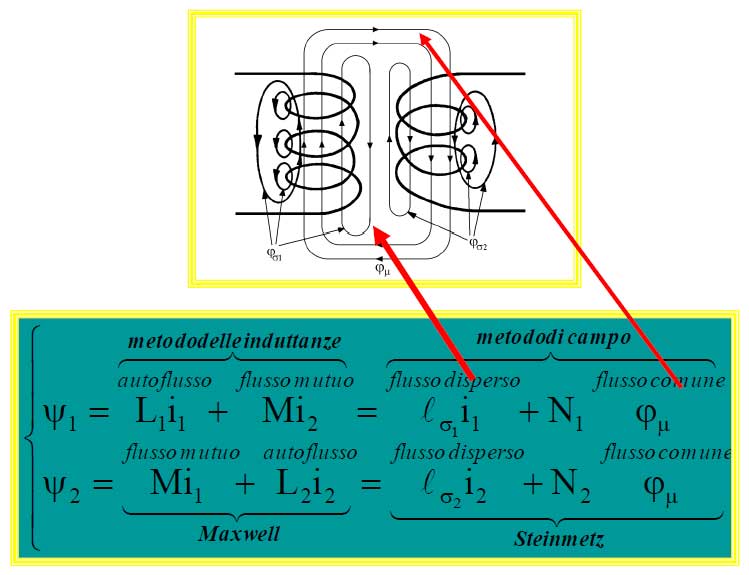Steinmetz sostituisce il metodo (esterno) delle induttanze (di Maxwell) con il (suo) metodo (interno) di campo.

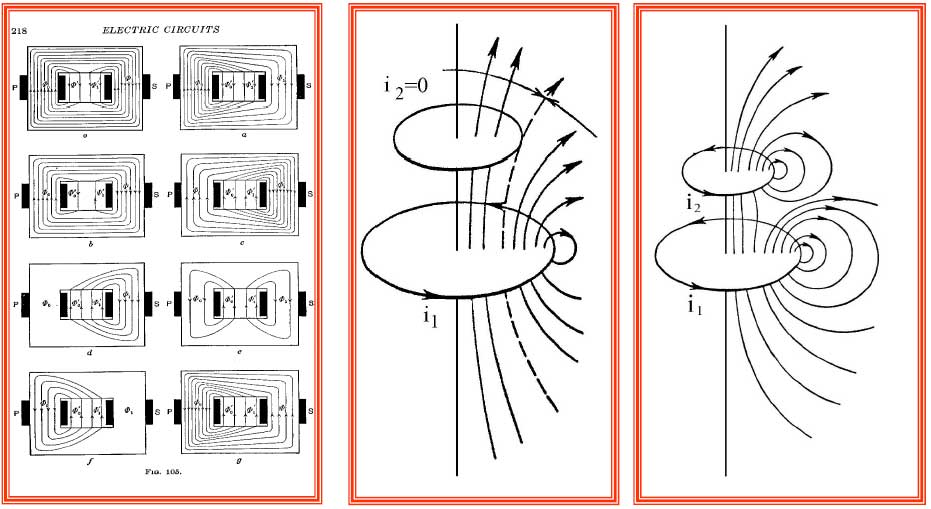
Ed ottiene così una prima parziale equivalenza interna. La soluzione sarebbe giunta solo nel 1930 con il paradosso di Weber

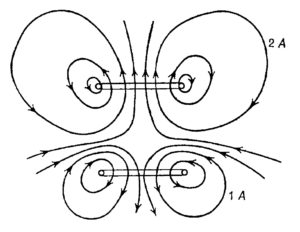
Matematico, ingegnere e filosofo, laureato in una Vienna influenzata dal pensiero di Mach, Boltzmann e Wittgenstein, Weber – a conferma della valenza strettamente maxwelliana dell’ingegneria elettromagnetica scientifica, – lasciò contributi cruciali sia nelle macchine elettriche che nelle telecomunicazioni.

Analoghe considerazioni, ma con anche maggior generalità, valgono poi per la teoria dei circuiti.

Sappiamo che in tal caso la transizione dalla continua all’alternata avviene in modo automatico, per semplice prolungamento analitico nel dominio
del tempo delle equazioni topologiche

E lo stesso, seguendo l’approccio  lagrangiano, avviene per le equazioni tipologiche.

Ma ben presto, con il crescere della frequenza, le cose non tornano più:

Sia le leggi topologiche che quelle tipologiche sembrano non trovare riscontro nell’evidenza sperimentale.

E sarà J. A. Fleming, uno dei discepoli di Maxwell ad osservare che:

Maxwell, by a process of extraordinary ingenuity, estended this reasoning [the method of Lagrange] from materio – motive force, quantities, currents, and electrokinetic energies of electrical matter, and in so doing obtained a similar equation of great generality for attacking electrical problems

Infine con Poincaré, le grosse difficoltà appariranno proprio in occasione, guarda caso, dell’experimentum crucis di Hertz.

Hertz sperimenta con alte frequenze ma, per calcolare la frequenza naturale con la formula di Kelvin, commette l’errore di avvalersi delle formule
stazionarie di Neumann.

A svelare l’enigma inatteso (regime quasi-stazionario) dell’approccio circuitale saranno le “percezioni” contenute in una lettera inviata da di Heaviside ad Hertz.

In realtà, già all’indomani del Treatise, le riflessioni che in seguito – concretamente – porteranno alle onde sono già iniziate. Avvalendosi di una lettura meccanica della corrente di spostamento, le onde elettromagnetiche sono già state dedotte (1862) dal modello meccanico dell’etere luminifero: il vortice molecolare di Maxwell!

Con il vizio di forma di una displacement current vissuta come una semplice metafora scientifica, la Dynamical Theory non viene assolutamente accettata e viene invece classificata come una Paper Theory.

Per parte sua, pur pienamente consapevole delle riserve che, in modo anche esplicito, sono avanzate dalla comunità scientifica, Maxwell non cerca di risolvere la questione tentando di riprodurre fisicamente le onde da lui stesso previste.

È significativa al riguardo, ancora una volta, un’affermazione di sir J.A. Fleming:

It was always a matter of surprise to me that Maxwell never seems to have attempted to obtain any experimental proof of the existence of the electromagnetic waves

Direttore del più prestigioso centro di ricerca del mondo, il Cavendish Laboratory, egli assolutamente non avverte mai, a differenza di quanto al suo posto, ad esempio, avrebbe invece fatto Faraday, l’esigenza di certificare sperimentalmente la veridicità della sua rivoluzionaria teoria.

Tant’è vero che quando, nel 1879, la prematura morte lo coglie, egli, attendendo alla II edizione del suo Treatise (poi pubblicata postuma da J.J. Thomson), sta occupandosi della parte tipografica.

Né, tutto sommato, di Onde Elettromagnetiche, egli scrive più che tanto nelle sue pubblicazioni. O parla, a Cambridge e al Cavendish, con Discepoli (e colleghi…).

Allo stato attuale, risulta assai difficile ravvisare le motivazioni che, relativamente ad un tema così cruciale, sono proprie, da parte sua, di un silenzio così esplicito, voluto e durevole. Due, al riguardo, sono, a tutt’oggi, le spiegazioni ritenute più plausibili. La prima ritiene che Maxwell fosse del tutto
estraneo allo studio delle onde elettromagnetiche e che il suo reale interesse fosse costituito invece dall’ottica. Addirittura, secondo tale lettura, per lui l’elettricità ed il magnetismo altro non sarebbero stati che uno strumento supplementare per ancor meglio esplorare e comprendere, nell’etere, l’essenza stessa dei fenomeni luminosi.

Per contro, secondo altri, Maxwell, come già in precedenza Faraday, si sarebbe addirittura servito dell’ottica per ancor meglio comprendere proprio l’elettricità ed il magnetismo. Difficile, a questo punto, riuscire a conciliare due posizioni così opposte. Tanto più che, data la mancanza oggettiva
di una qualunque concreta documentazione al riguardo, di fatto entrambe le interpretazioni non possono considerarsi che una semplice congettura.

Un dato “singolare” rimane comunque assolutamente certo e non tralasciabile: Maxwell non cercò mai, magari anche solo realizzando un “semplice” circuito oscillante, di generare onde elettromagnetiche per via elettromagnetica diretta.

Per quale motivo? Anche in tal caso, nel cercare una possibile risposta, trattandosi nuovamente di una congettura, la prudenza non può che rimanere
assolutamente d’obbligo.

Il dato certo, alla luce dei fatti oggettivi, è comunque che per lui luce ed onde elettromagnetiche altro non furono che manifestazioni “distinte” di uno medesimo stato di sforzo e di moto in atto all’interno dell’etere.

In quest’ottica, appare ragionevole ritenere che egli, tralasciando a priori ogni possibile valenza elettromagnetica, possa aver pensato di generare onde per via meccanica diretta.

Abbia ritenuto cioè di innescare, in senso meccanico stretto, processi vibratorî nelle molecole stesse dell’etere. In altri termini, l’onda, luce compresa, è incontestabilmente di natura elettromagnetica, ma la sua genesi, avvenendo nell’etere, non può che essere meccanica.

Per ora continua però a coglierlo nel suo senso meccanico più immediato, onde luminose comprese. Del resto è ben noto come la presenza dell’aggettivo Dynamical accanto alla sua Theory fosse strettamente legato alla sua più che ferma necessità di esser preso sul serio quando, a proposito dell’energia cinetica e potenziale in gioco, egli pretendeva di considerarla di natura strettamente meccanica.

Nessun circuito elettrico, all’interno del suo laboratorio, appare dunquenecessario per il meccanicista Maxwell.

Il quale, se in seguito, meditando da epistemologo sul portato conoscitivo del suo Grande Disegno della Natura, avrebbe finito con il considerare l’etere nient’altro che «un nome inventato per dare un soggetto al verbo ondulare». Finalmente, a chiarire un approccio circuitale fino a quel momento erroneamente vissuto come del tutto estraneo alla Dynamcal Theory, interviene il paradigma maxwelliano.

La fase iniziale di ricerca scientifica sulla generazione e ricezione delle onde elettromagnetiche risulta complessivamente collocabile tra il 1879 ed il 1883 ed è interamente dovuta al lungo ed appassionato lavoro (talvolta non esente da errori) di due Maxwellians: Oliver Lodge e George Fitzgerald.

Lodge e Fitzgerald si incontrano, entrambi ventisettenni, nel 1878, al Convegno di Dublino della British Association. Discepoli entrambi di Maxwell, il primo ha anche avuto il privilegio di udire il Maestro nel 1873, in occasione di un seminario da questi tenuto a Bradford; ne consegue, in particolare, una lettera di Lodge a Maxwell, cui lo scienziato scozzese non manca di rispondere con un messaggio da Lodge stesso in seguito giudicato «humorous and quite long». O. Lodge giunge vicinissimo alla generazione di onde elettromagnetiche mediante un circuito elettrico, egli ottiene studia però tali perturbazioni lungo i conduttori e non nello spazio vuoto circostante, la conseguenza più immediata del lavoro svolto da Lodge è tuttavia rappresentata dall’opera di coinvolgimento da lui compiuta sull’amico FitzGerald, il quale

discharging condensers through circuits of small resistance, to obtain sufficiently rapid alternating currents

Ritiene che la generazione per via circuitale di onde elettromagnetiche debba considerarsi impossibile.

Ma poi, nel 1883, in quello – di una pagina e mezza – che certo deve essere considerato l’articolo fondante più breve della storia della scienza, egli associa un’ onda elettromagnetica ad un circuito oscillante e ne calcolo la potenza irradiata:

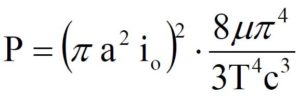
Lo spazio cessa di essere geometrico e, compromesso con l’evento, diviene fisico.